고정 헤더 영역
상세 컨텐츠
본문

ABSTRACT
고성능의 DNN(Deep Neural Network)은 학습에 상당한 시간이 소요되기 때문에 훈련 시간을 줄이는 방법으로 뉴런들을 정규화(Normalization)하는 방법이 있다. 그 중 하나인 Batch Normalization은 training case의 mini-batch에서 뉴런에 대한 총 input 분포를 사용하여 평균과 분산을 계산한다. 이 방법은 DNN의 훈련 시간을 대폭 줄일 수 있지만 mini-batch 사이즈에 영향을 받으며 RNN(Recurrent neural Network)에서의 활용 방안이 불명확하다.
이에 본 논문은 Layer Normalization을 제시하여, 단일 훈련 사례에서 layer의 summed input으로부터 normalization에 사용되는 모든 평균과 분산을 사용해서 batch normalization을 layer normalization으로 변환한다. Layer normalization과 batch normalization 두 정규화 기법 모두 각 뉴런마다 adaptive bias와 gain 변수를 보유한다. 하지만 layer normalization의 경우 Train 모드와 Test 모드에서 똑같이 동작하고 RNN의 은닉층(hidden layer)의 안정화에 효과적이어서 훈련 시간을 크게 줄일 수 있다고 설명한다.
INTRODUCTION
Stochastic Gradiend Descent(SGD)에서 훈련된 DNN은 computer vision(CV)와 speech processing에서 놀라운 성과를 보여왔다. DNN은 훈련에 많은 시간이 소요되는데 많은 기계를 이용해서 스피드를 올릴 수는 있지만 복잡한 소프트웨어가 필요하다. Batch normalization은 DNN에서 추가적인 정규화 단계를 포함하여 훈련 시간을 줄였고, Feed Forward Network에서 각 layer마다 정규화에 이용되는 통계치를 저장하고 거듭 사용하여 많이 활용되었다.
그러나 RNN의 경우 input의 길이가 달라지기 때문에 시간 단계에 따라 다른 통계치를 써야 한다. 이러한 특성 때문에 Batch Normalizatoin은 RNN에 적용될 수 없고, Layer Normalization은 각 layer에서 바로 은닉층 input의 정규화 통계치를 계산할 수 있기 때문에 RNN에 적용시킬 수 있다.
* feed forward network : 노드 사이의 연결이 주기를 형성하지 않슨 인공 신경망
- Batch normalization : 각 feature의 평균과 분산을 구해 batch에 있는 각 feature를 정규화
- Layer normalization : 각 input의 feature들에 대한 평균과 분산을 구해 각 층의 input을 정규화
Backgrounds
Feed Forward neural network


Batch normalization
딥러닝은 특정 layer 가중치의 gradient가 이전 layer 출력값에 크게 의존한다는 문제점이 있는데, batch normalzation은 batch의 모든 샘플에 대해 은닉층의 각 뉴런으로 들어오는 input들의 총합을 정규화하여 이 문제를 해결할 수 있다.


l번째 layer에서 i번째 input 총합에서 그들의 분산에 따라 그 총합을 rescale(크기 재조정)한다. 즉, Batch normalization은 학습 과정에서 Batch마다 평균과 분산을 활용하여 데이터의 분포를 정규화하는 과정을 의미한다.
* 추가 설명

위의 수식으로 다시 살펴보면 미니배치 B = {x1, x2, ... xm}이라는 m개의 입력 데이터의 집합에 대해 평균과 분산을 구한 후 입력 데이터를 평균이 0, 분산이 1이 되게(적절한 분포가 되게) 정규화한다. 입실론 값은 작은 값(예를 들어 10^e-7)으로, 0으로 나누는 사태를 예방하는 역할이다. 위 식은 mini-batch input 데이터를 평균 0, 분산 1인 데이터로 변환되는 것을 의미한다.
Layer Normalization
Covariance shift는 일반적으로 특정 layer output의 변화가 다음 layer로의 input 총합에 꽤 상관있는 변화를 일으키는 것을 뜻한다(ReLU 등). 이러한 covariance shift의 문제는 각 layer에서의 input 총합의 mean과 variance를 고정시킴으로써 해결할 수 있다. 따라서 아래와 같은 과정을 통해 특정 layer의 모든 은닉층 뉴런에 대한 layer normalization을 진행할 수 있다.

* H : hidden layer number
방정식 2와 3의 차이는 layer normalization에서 모든 은닉층이 같은 정규화 변수를 갖고 있다는 점이다.
layer normalization은 mini-batch size에 제약이 없기 때문에 하나의 객체에서도 정규화 될 수 있다.

* 출처 : https://github.com/dsc-sookmyung/2021-DeepSleep-Paper-Review/blob/main/Week3/layernormalization.pdf
Layer normalized recurrent neural network
NLP 문제에서는 훈련 샘플마다 문장의 길이가 달라지는 것이 일반적인데, RNN은 모든 시간 단계에서 같은 weight를 사용하기 때문에 이러한 상황에 효과적이다. Batch Normalization을 RNN에 적용하면 매 시간 단계마다 다른 통계량을 계산하고 저장해야 하기 때문에 test 문장의 길이가 train 문장들보다 길 때 통계량을 이용할 수 없다는 문제가 발생한다. 반면 Layer Normalizaion은 현재 시간 단계에서 특정 layer로 들어오는 input 총합의 통계량에 기반하여 위와 같은 문제가 생기지 않는다. 아래 식에서의 계수들은 방정식 3의 계수들을 recentering과 rescaling을 거쳐서 구한다. 표준적인 RNN에서는 input 총합의 평균 크기를 recurrent 층에 넣으려는 경향이 있지는데, layer normalization에서는 정규화가 모든 input 총합의 rescaling에 불변하게 만들기 때문에 hidden-to-hidden 역학에서 더 안정적이다.


* W_hh : recurrent hidden to hidden weights / W_xh : bottom up input to hidden weights

* 출처 : https://github.com/dsc-sookmyung/2021-DeepSleep-Paper-Review/blob/main/Week3/layernormalization.pdf
Related work
[1] Batch Normalization on RNN
기존에 RNN에 Batch Normalization을 적용하려는 시도가 있었고 해당 연구진은 각 시간 단마다 독립적인 normalization 통계량을 사용하였고, gain 파라미터를 0.1로 초기화하였을 때 모델의 성능을 극대화할 수 있었다.
[2] Weight Normalization
Weight Normalization은 normalization 기법 중 하나로 variance 대신에 앞단 weight들의 L2 norm이 뉴런 input 총합을 정규화하는 것에 이용되는 것으로 L2 norm을 이용한 normalization을 의미한다.
Analysis

Invariance under weights and data transformations
layer normalization은 batch normalization과 weight normalization과 관계되었는데, 이들 값들이 다르게 계산될 수 있지만 그 방법은 input 총합 a_i를 mu와 sigma를 통해서 정규화하는 것으로 요약할 수 있다.
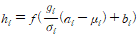
* b : adaptive bias / g : gain parameter -> 정규화 후 각 뉴런에서 학습
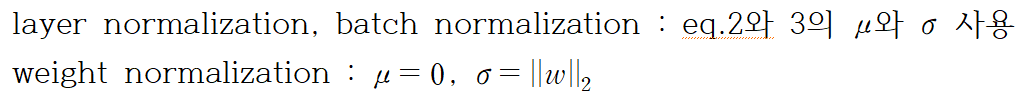
Weight rescaling & recentering
BN(Batch normalization)과 WN(Weight normalization)에서 단일 뉴런 w_i를 rescaling하는 것은 효과가 없다. 이들의 가중치 벡터가 delta에 의해 scale된다면, 이들의 평균과 분산도 delta에 의해 결정된다고 할 수 있다. 정규화된 input 총합은 scaling 후에도 같으므로 BN과 WN에서 가중치 rescaling에 대해 invariant(불변)하다.
반면, LN(Layer normalization)은 단일 가중치 벡터 scaling에 불변하지 않으며, 전체 가중치 행렬 rescaling에 대해 불변하고 가중치 행렬의 입력되는 가중치 값의 변화에도 불변하다. 만약 정규화가 가중치 이전에만 적용된다면, 모델은 가중치 rescaling과 recentering에 대해 불변하지 않다.

Data rescaling and recentering
모든 정규화 방법은 data set rescaling에 대해 불변하다. 즉, 뉴런의 input 총합이 변화에 대해서 일정하다고 할 수 있다. LN은 각각 훈련 케이스의 rescaling에 불변하는데, 평균과 분산이 오직 현재 입력 데이터에 대해서만 의존하기 때문이다.

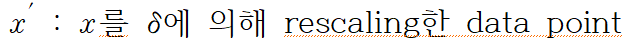
LN에서 각각의 데이터를 rescale하는 것은 모델 예측을 변화시키지 않는다. LN의 가중치 행렬의 recentering과 유사하게, BN에서 데이터셋의 recentering도 불변함을 알 수 있다.
Geometry of parameter space during learning
학습은 우리가 조사한 parameter의 recentering과 rescaling의 불변성과 달리 모델이 같은 근본적인 함수를 뜻하더라도 다른 매개변수화에서 매우 다르게 행동할 수 있다. 우리는 기하학적 학습과 parameter space의 manifold(다양체)에서 정규화된 scalar인 sigma가 학습률을 낮추고 학습을 안정화시킴을 보여줄 것이다.
Riemannian metric(리만 계량 / 리만 다양체)
통계적 모델에서 학습가능한 parameter들은 모델의 모든 가능한 입출력 관계를 이루는 smooth한 다양체를 형성한다. 출력이 확률분포인 모델에서 분리된 두 점을 측정하는 방법은 그들의 모델 출력 분포 사이의 Kullback-Leibler divergence이다. KL divergence metric 안에서 모수 공간은 리만 다양체이다.

출처 : https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence
리만 다양체에서 곡률은 리만 다양체에서의 2차항 형태인 ds^2에 의존한다. ds^2은 parameter space의 한 점에서 접선 공간의 무한 최소 거리이다. KL하의 리만 metric은 fisher information을 사용하여 2차 테일러 확장에서 잘 근사되는 것으로 나타났다.
* fisher information


정규화된 GLM에서의 기하학
GLM(generalized linear model)은 가중치 벡터 w와 편향 scalar b를 사용하여 exponential family로부터 출력 분포를 매개변수화시키는 것으로 간주될 수 있다.
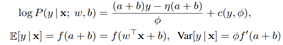

H 차원을 가지는 출력변수 y가 GLM과 logP함수에 대해서 모델되었다고 하자. W를 weight matrix라 하고, b를 H 길이의 bias vetcor, vec를 Kronecker vector라고 정의할 때, 피셔 정보 행렬은 다음과 같이 표현된다.
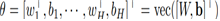
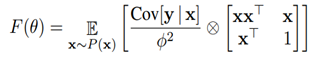
* 원래 모델의 평균과 분산을 통해, a(input 총합)에 정규화 방법을 적용하여 정규화된 GLM을 얻음
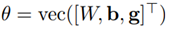

가중치 벡터 성장에 따른 학습률 감소
정규화된 GLM 함수에서의 w_i 방향으로의 F는 sigma_i에 의해 scale된다. 만약, 가중치 벡터의 크기가 2배 커진다면, 출력값이 같더라도 피셔 행렬은 달라진다. sigma_i도 2배가 됐기 때문에 가중치 방향으로의 곡률은 1/2배가 될 것이다.결과적으로, 정규화 모델에서 같은 변수 업데이트에서 가중치 벡터의 크기는 효과적으로 가중치 벡터의 학습률을 조절한다.
Incoming weight 크기 학습
정규화 모델에서 incoming weight의 크기는 gain parameter에 의해 조절된다. 논문에서는, 정규화된 GLM에서 gain parameter를 업데이트하는 것과 학습 중 원래 매개변수화 하에서 가중치의 크기를 업데이트하는 것 사이에서 모델 출력값이 어떻게 변화하는지 관찰한다. 표준 GLM에서 incoming weight에 크기에 따른 rimannian metric이 input의 크기에 의해 scale됨을 보여준다. 반면, BN과 LN 모델에서 gain parameter 학습은 오직 예측 오차의 크기에 의존한다. 즉, 정규화 모델에서 입력되는 가중치 크기 학습이 표준 모델보다 입력 및 매개변수 scaling에 더 강력하다.
Experimental Results
Image-sentence Ranking, question answering 등 총 6가지 방법들에 대해 LN의 효과 확인
adaptive gain 1, bias 0 설정
Order Embeedings of images and language(Image-sentence ranking)
위 방법에 대해 LN 적용했을 때와 아닐 때를 비교
매 300번의 반복마다 Recall@K의 값을 비교하고, 모델 성능이 발전했다면 모델을 업데이트함.
* Recall@K : k개 출력 결과에 대한 Recall을 계산한 것으로, 사용자가 관심있는 모든 아이템 중에서 모델이 출력한 아이템 k개가 얼마나 포함되는지 비율
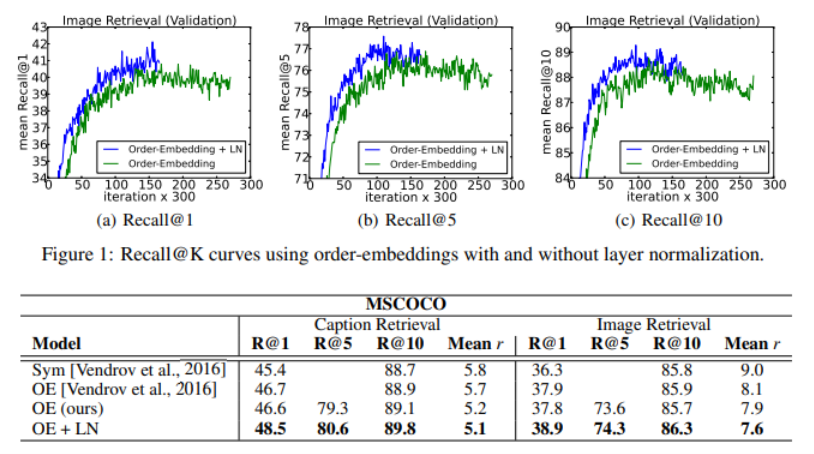
Order-embedding에 LN을 해주었을 때 반복당 연산 속도가 증가했고, LN이 없을 때와 비교해 결과 값이 수렴하는데 약 60% 정도의 시간만 소요된 것으로 측정, 즉, 수렴을 더 빨리 해 빠르게 계산 결과를 얻을 수 있었다.
Teaching machines to read and comprehend(Question answering)
machine에게 CNN 말뭉치로 된 글을 읽고 이해하도록 학습 / LN과 BN의 성능 비교
위 실험에서의 machine : 질문을 machine에 입력하면 문장의 빈칸을 채움
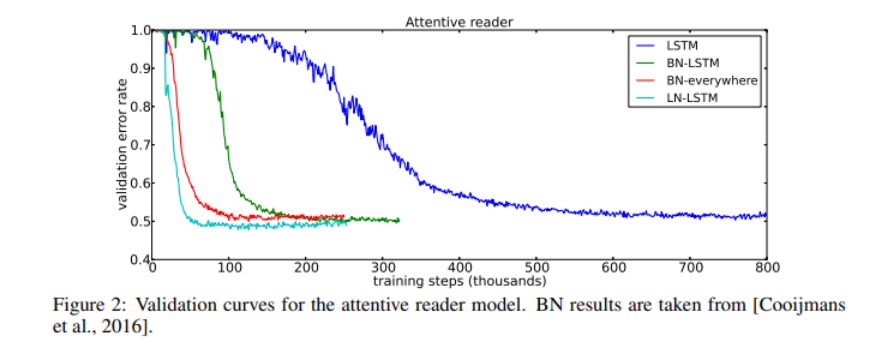
Long Short Term Memory(LSTM)에 LN을 적용해준 결과가 BN등 다른 방법들에 비해 수렴 속도도 빠르고, 유효 오차 또한 제일 낮은 것을 알 수 있다.
Skip thought Vector(Contextual language modeling)
skip thought vector : skip-gram model의 일반화 버전, 중심 단어를 통해 주변 단어 예측하는 모델의 확장형
LN이 training단계를 증속할 수 있는지 비교
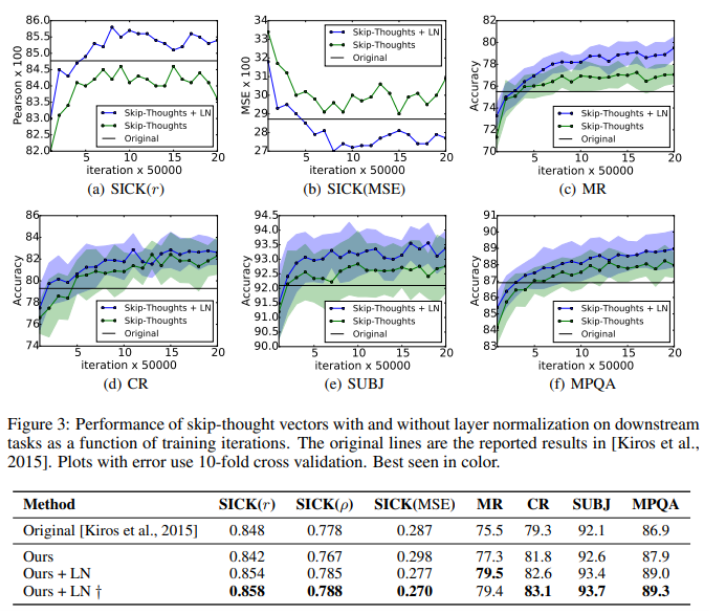
기존 모델에 비해 LN을 적용했을 때, 1백만 번의 반복 이후 상관계수는 높고, 평균제곱오차(MSE)는 낮아지고, 예측 정확도는 상승하였다. 즉, skip-thought vector 모델의 예측 성능이 LN을 해주었을 때 상승함을 알 수 있다.
Modeling binarized MNIST using DRAW(Genarative modeling)
MNIST 데이터셋에 DRAW(Deep Recurrent Attention Writer) 모델 적용
64개의 glimpse와 256개의 LSTM 은닉의 LN효과를 측정
전체 dataset을 5만개의 training data, 각각 1만개의 validation, test 데이터로 분할해서 측정 실시
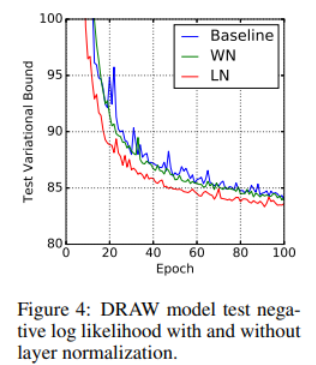
첫 100개 epoch에서 test variational bound를 나타낸 그래프를 보면, LN을 적용한 방법이 기존 모델에 비해 2배 정도 빠르게 수렴하는 것을 알 수 있다.
Handwriting sequence generation
길이가 긴 수열에서 LN이 효과적임을 보이기 위해 handwriting generation 문제 활용
3개 은닉 층에 400개 LSTM cells, 3개의 입력 layer, 20개의 bivariate Gaussian mixture를 출력하는 output layer로 된 모델 Batch수는 작지만 문장 하나가 긴 문장을 입력하기에 은닉 층의 구조가 안정되어 있는 것이 중요

실험 결과 LN을 적용했을 때 Negative Log Likelihood이 낮아질 뿐만 아니라, 더 빠르게 수렴한다.
Permutation invariant MNIST(MNIST classification)
LN은 re-scaling에 상관 없이 invariant한데, 이는 내부의 은닉 층에는 좋은 점으로 작용한다. 하지만, 이러한 특성은 logit을 이용하는 출력 층에 단점으로 작용하기도 한다. 따라서, LN의 적용은 출력 층을 제외하고 완전히 연결된 (fully-connected) 은닉 층에 적용해야 한다.

Feed-forward networks에 LN을 적용 했을 때, batch-size에 더욱 강력해지며, 빠른 수렴 속도를 보이는 것을 알 수 있다.
Convolutional network
합성곱 신경망(CNN) 은 인간의 시신경을 모방한 신경망 구조로, 시각정보 처리에 활용된다. 상기된 방법들 전부에서 LN이 매우 효과적임을 알 수 있지만, LN을 적용했을 때 영상/이미지 데이터에서 이미지의 경계에 위치한 receptive fields에서는 모델의 성능이 매우 미미했고, 당 논문에서도 발전 과제로 제시하였다.
* receptive fields : 수용 영역 각 단계의 입력 이미지에 대해 하나의 필터가 커버할 수 있는 이미지 영역의 일부
'2023 Summer Session > DL' 카테고리의 다른 글
| [4주차/DL2팀/논문 리뷰] (0) | 2023.08.08 |
|---|---|
| [4주차 / DL 1팀 / 논문 리뷰 ] Deep Residual Learning for Image Recognition (0) | 2023.08.03 |
| [3주차/DL1팀/논문 리뷰] Batch Normalization (0) | 2023.07.27 |
| [2주차/DL 2팀/논문 리뷰] ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION (0) | 2023.07.20 |
| [2주차 / DL 1팀 / 논문 리뷰] Neural Networks for Machine Learning (0) | 2023.07.20 |





댓글 영역