고정 헤더 영역
상세 컨텐츠
본문
# Abstract
고차원의 매개변수와 노이즈가 있는 objective function과 관련하여 최적화 기법이 요구되어 왔으며 본 논문은 이에 대한 답으로 Adam을 제시한다. Adam의 개념과 알고리즘 그리고 Adam과 관련 있는 알고리즘 – AdaGrad, RMS PROP 과 더불어 infinity norm을 기반으로 변형된 형태인 AdaMax 또한 본 논문에서 다루고 있다.
Adam 은 2개의 *lower-order moments의 추정치를 기반으로 *stochastic objective functions을 *first-order gradient-based로 최적화하는 알고리즘이다.
해당 알고리즘은 구현이 쉽고, 효율적인 계산으로 메모리 요구사항이 거의 없다.
또한 *gradient의 diagonal rescaling에 독립적이며 gradient에 noise가 많거나 sparse한 경우에도 적합하다.
*low-order moments : 저차 모먼트
*stochastic objective functions : random sampling하여 매번 loss function 값이 달라지는 함수, 일종의 Loss function
*first-order gradient-based : 1차 함수 기울기
*gradient의 diagonal rescaling에 독립적
: 대각성분의 재조정에 독립적, gradient를 차원 별로 독립적으로 rescaling 하는 것에 영향을 받지 않는다
→ 파라미터 별 학습률 달리 조정 가능
# Introduction
Adam은 Stochastic objective function에 대한 first-order gradient-based optimization 기법 중 하나이다.
(참고로 본 논문은 다차원 매개변수가 포함된 stochastic objective에 초점을 두며 first-order methods 측면에서 논의된다)
Adam은 Adaptive Moment Estimation에서 비롯된 이름으로 first-order gradients에 기반하여 연산량이 적고 효율적인 stochastic optimization 알고리즘이다. 이 방법은 gradient의 첫번째 그리고 두번째 moment의 추정치로부터 파라미터들 각각의 Learning rate(학습률)를 계산한다. Adam은 최근 많이 활용되는 두 방법인 AdaGrad와 RMSProp의 장점을 통합하여 설계되었다.
*AdaGrad의 경우 sparse gradients에 적합하고 RMSProp은 on-line 상황 그리고 non-stationary setting에 적합
= 이 둘의 장점을 합친 것이 Adam이다.
# Related Work
(1) AdaGrad : 가중치(weight)의 업데이트 횟수에 따라 learning rate을 조절하는 옵션이 추가된 optimization 알고리즘으로 SGD(Stochastic Gradient Descent)와 달리 parameter별로 learning rate을 다르게 적용할 수 있다.
-업데이트가 많이 되지 않는 weight는 Learing rate(혹은 step size)를 크게 하여 빠르게 loss 값을 줄이고
-업데이트가 많이 된 weight들에 대해서는 Learing rate를 작게하여 세밀하게 값을 조정한다.


위 수식에서 Learning rate과 관련된 부분에서 모든시점의 gradient 제곱의 합이 반영된다.
이러한 이유에서 t 즉 시점이 충분히 커지면 gradient가 작음에도 거듭 더해지면서 학습이 진행될수록 learning rate가 0으로 수렴한다는 단점이 있다. 즉 과거의 기울기를 제곱하여 계속해서 더해나가기 때문에 학습을 진행할수록 업데이트 정도가 약해지며 loss 값이 어느순간 더 이상 줄지 않는 문제가 발생한다. 이러한 문제를 해결한 것이 RMSProp 알고리즘이다.
(2) RMSProp: AdaGrad와 달리 exponential moving average를 적용하여 최근 gradient에 더 높은 가중치를 부여하는 알고리즘이다. 과거의 모든 기울기를 균일하게 적용하는 것이 아닌 현재에 가까운 기울기 정보를 크게 반영하는 것으로 해당 파라미터를 decaying rate라고 부른다. 결과적으로 RMSProp은 learning rate가 0으로 수렴하는 문제가 발생하지 않는다.


# Algorithm
Adam은 moment를 계산하는 부분과 bias로 이를 조정하는 두 부분으로 나뉠 수 있다.
Moment의 경우 Momentum이 적용된 first moment와 AdaGrad, RMSProp이 적용된 second moment로 구분하고 있다.

초기에 필요한 파라미터는 아래 4가지이다.
1. Stepsize α (Learing Rate, 학습률)
2. Decay Rates β1, β2 : Exponential decay rates for the moment estimates (0~1 사이의 값)
3. Stochastic Objective Function f(θ), θ : parameters (weights)
4. initial Parameter Vector θ0
함수 f는 가중치 θ에 대한 stochastic 함수이다. 따라서 stochastic하게 optimization을 수행하므로
우리는 f의 기대값인 E[f]의 최소값을 찾는 문제를 해결하는 것이 목표이다. g는 f를 θ에 대해 미분한 gradient 함수이다.
먼저 Momentum의 개념이 반영된 m과 v가 update하는 부분을 살펴보자.

앞서 언급했듯 Momentum의 개념이 반영된 m과 RMSProp(AdaGrad) 부분이 반영된 v의 식이 제시되어 있으며
각각 first moment estimation, second moment estimation이라고 칭하고 있다.
(1) First moment estimation인 m
: 현재까지의 gradient들의 가중 평균이다. 이 평균값(기대값)은 매번 바뀌며, 평균값은 exponentially moving averages of the gradients, 즉 지수적으로 움직인다.

(2) Second moment estimation v
: 지수적으로 움직이는 기울기의 제곱값의 가중 평균(exponentially moving averages of the squared gradient)이다.

하지만 이 moving averages들, m과 v는 초기에 0으로 설정되어 있기 때문에, moment를 0에 치우치게 추정하려는 경향이 생긴다. 이러한 initialization bias 문제를 해결하기 위해 bias correction 부분이 필요하다.
# Initialization Bias Correction

Bias Correction을 적용한 first, second moment estimation은 위와 같다. 각 모멘트를 1-B로 나눈 값이다.
아래 과정을 통해 각 모멘트를 1-B로 나누어 Bias Correction을 진행하는 것을 확인할 수 있다.


Second moment estimation v를 통해 살펴보면, 우리는 second moment의 기댓값을 구해야하고 궁극적으로는 v의 기댓값이 g2 (g^2)의 기댓값과 같게 하고자 한다. 결과적으로 v의 기댓값을 1-Bt 으로 나누어주면 g2의 기댓값과 유사해지므로 이를 통해 bias 문제를 해결할 수 있다.

# Experiments
(1) LOGISTIC REGRESSION
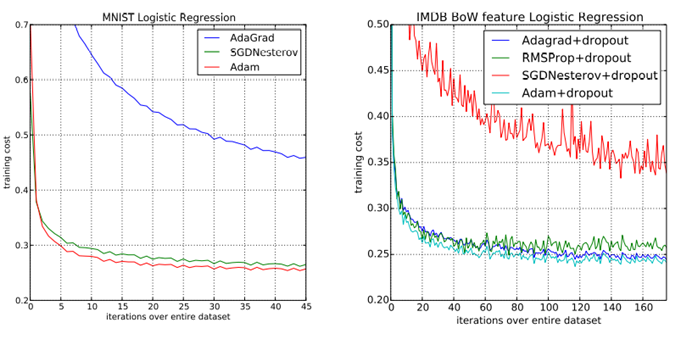
Optimizer에 따른 training cost를 살펴보았을 때 로지스틱 회귀 결과 Learning rate만 조절하는 AdaGrad보다 Adam의 성능이 월등히 뛰어남을 확인할 수 있다. MNIST 데이터와 IMDB데이터 모두 Adam의 training cost가 0으로 수렴함과 동시에 robust함을 확인할 수 있다.
(2) MULTI-LAYER NEURAL NETWORKS


Multi-layer neural networks 분석을 통해 drop-out regularization을 적용했을 때의 optimizer 성능을 비교해보면 Adam이 가장 빠르게 수렴함을 확인할 수 있다. 2번째 그래프에서도 dropout을 적용하지 않은 optimizer 중에서 Adam이 제일 수렴 속도가 빠를 뿐 아니라 dropout을 적용한 optimizer 중에서도 Adam이 제일 수렴 속도가 빠름을 알 수 있다.
*dropout : 훈련 과정에서 신경망의 일부 뉴런을 무작위로 비활성화
어떤 특정한 설명변수 Feature만을 과도하게 집중하여 학습함으로써 발생할 수 있는 과적합(Overfitting)을 방지
(3) Bias Correction Term

위 그래프에서 초록색 그래프는 bias correction terms이 없는 RMSProp에 해당하고 빨간색 그래프는 bias correction terms이 포함된 경우이다. 결과적으로 bias correction term을 적용하지 않았을 경우 B2가 1에 가까워질수록 불안정함을 확인할 수 있다. B2가 1에 가까울수록 bias correction term이 효과가 더욱 극대화되었다. 실험결과를 요약하자면 Adam 알고리즘은 하이퍼파라미터 설정에 상관없이 RMSProp 이상의 성능을 보였다.
# Extenstion
Adam에서는 개별 가중치를 업데이트하기 위해 과거와 현재의 gradient의 L2 norm을 취하였다.
이때 L2 norm을 Lp norm으로 변경할 수 있는데 이것이 Adamax이다.
p값이 커질수록 수치적으로 불안정해지나, p를 무한대라고 가정(infinity norm)하면 간단하고 stable한 알고리즘이 된다.
L2 norm을 사용하여 가중치 업데이트를 스케일링하는경우 보통 그레이디언트의 제곱의 누적 값을 저장하여 계산한다. 반면 Adamax에서는 infinity norm을 사용하여 그레이디언트의 절대값의 누적 값을 저장하여 계산한다.
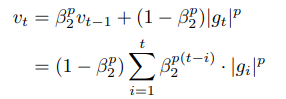

second moment의 수식을 변경하고, bias correction 계산은 빠진 것을 확인할 수 있다.
# Conclusions

본 논문은 Stochastic objective function의 optimization을 위한 단순하고 효율적인 최적화 알고리즘인 Adam을 소개하였다. First-order optimization 알고리즘으로 단순하고 계산 효율성이 높으며 대량의 데이터셋과 다차원의 파라미터에 대한 머신러닝의 문제 해결을 도울 수 있다. Adam은 AdaGrad가 Sparse gradients를 다루는 방식과 RMSProp이 non-stationary objectives를 다루는 방식을 조합하여 두 알고리즘의 장점을 조합하였다. 실험을 통해 SGD, RMSProp에 비하여 Adam 알고리즘의 상대적으로 뛰어난 성능을 확인할 수 있었다.
'2023 Summer Session > DL' 카테고리의 다른 글
| [4주차/DL2팀/논문 리뷰] (0) | 2023.08.08 |
|---|---|
| [4주차 / DL 1팀 / 논문 리뷰 ] Deep Residual Learning for Image Recognition (0) | 2023.08.03 |
| [3주차/DL1팀/논문 리뷰] Batch Normalization (0) | 2023.07.27 |
| [3주차/DL2팀/논문 리뷰] Layer Normalization (0) | 2023.07.26 |
| [2주차 / DL 1팀 / 논문 리뷰] Neural Networks for Machine Learning (0) | 2023.07.20 |





댓글 영역