고정 헤더 영역
상세 컨텐츠
본문
github 연동하여 ViTAE pretrained model 을 활용해 보고자 한 코드 입니다.
추가로, DIFFUSION BASED IMAGE TRANSLATION USING DISENTANGLED STYLE AND CONTENT REPRESENTATION 논문을 리뷰해 보았습니다.
https://openreview.net/pdf?id=Nayau9fwXU
0. Abstract
diffusion 모델의 한계라고 언급되는 stochastic nature 란 게 뭘까? 이 성질때문에 reverse diffusion 하는 동안 이미지의 내용을 유지하기 힘듦.
<aside> 💡 reverse diffusion이란?
잠재 공간에서의 확률 분포를 따라가면서 데이터를 생성하는 과정
</aside>
→ DiffuselT 등장!
ViT 의 MHSA 를 차용해 content preservation loss 에 사용
이미지를 이용한 스타일 변환은 디노이즈된 샘플과 타겟 이미지 간의 CLS 토큰 매칭으로, 텍스트를 이용한 스타일 변환은 CLIP loss 로
novel semantic divergence loss & resampling 을 활용해 semantic change 를 가속화함. sampling 속도를 높임.
<aside> 💡 semantic change 란? text-to-image task 에서 언어적 정보와 시각적 정보 사이의 갭을 이어주는 역할
</aside>
1. Introduction
텍스트 기반 이미지 생성은 GAN 기반 , OOD 이미지 생성 시 semantic change 가 잘 컨트롤되지 않음.
text-to-image 에서 score-based 생성 모델이 sota이지만 이미지 변환에서는 아님.
구조 정보를 유지하고 의미 정보만 바꾸는 게 가장 중요한 문제.
인풋과 타겟 도메인 이미지가 매치되는 contitional한 diffusion 모델의 경우엔 문제가 되지 않지만 이런 경우는 거의 없음.
unconditional 한 모델은 의미를 보존하는 데 어려움을 겪음.
pre-trained ViT 로 부터 얻은 loss function 이용 + content 정규화는 MHSA 의 중간 키 + style 정규화는 DINO ViT 의 CLS
sampling 과정에서 인풋의 중간 키와 디노이즈된 이미지 사이의 유사 및 대조 loss 를 이용해 구조 정보 보존
이미지 내용을 바꾸지 않고 텍스트, 이미지 기반 모두 변환하는 unconditional diffusion 모델은 우리가 처음!
2. Related Work
- Text-guided image synthesis
CLIP 은 object generation, style transfer, object segmentation 등 여러 task 에서 많이 쓰임. 이미지 생성에서도 CLIP 이용.
but, Style-GAN 베이스 모델은 사전 훈련된 데이터 도메인에 한정됨. & VQGAN 도 이미지 퀄리티 떨어짐.
DDPM(Denoising Diffusion Probabilistic Model) 과 같은 점수 기반 모델로 텍스트 기반한 퀄리티 좋은 이미지 생성하려고 했지만 텍스트와 입력이미지가 잘 엉키지 않아서 이미지 변환에 있어서는 아쉬웠음.
DiffusionCLIP 이 reverse diffusion 단계에서 DDIM 샘플링과 pixelwise regularization 을 통해 해결하려고 했지만 파인튜닝이 필요하다는 치명적 단점이 있음.
DDIB : deterministic probability flow ODE formulation 이용
- Single-shot Image Translation
하나의 타겟이 있는 이미지 변환은 이미지 style transfer 에 주력
StyleGAN adaptation 을 이용한 방법 한계 : 도메인 한정적
처음보는 이미지를 타겟의 semantic 으로 변환하는 것은 또 이미지 퀄리티 떨어짐.
Splicing ViT : pretrained DINO ViT 를 이용해 구조를 유지하면서 타겟 도메인으로 의미 변환 가능하게 함.
3. Proposed Method
DDPM SAMPLING WITH MANIFOLD CONSTRAINT
guided_diffusion / gaussian_diffusion.py
ddpm
- & 2) 모두 마르코프 체인에 해당
- forward : 깨끗한 이미지 → 점차 가우시안 노이즈 추가 $q(x_t|x_{t-1})$
$q$ : diffusion process (노이즈화되는 과정) (from data to noise )
$x_0 = clean\,image ,\,x_T=$가우시안 노이즈 그 자체
$$ q(x_T|x_0) := \Pi_{t=1}^T, \quad q(x_t|x_{t-1}) := N(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_tI) $$
def get_named_beta_schedule
$\{\beta\}_{t=0}^T$ : variance schedule
$\alpha_t := 1-\beta_t$, $\bar{\alpha_t} := \Pi_{s=1}^t\alpha_s$
variance schedule 을 이용하여 scaling을 한 후 더해줌.
$\sqrt{1-\beta_t}$ 로 scaling하는 이유는 variance가 발산하는 것을 막기 위함.
$$ x_t = \sqrt{\bar{\alpha_t}}x_0 + \sqrt{1-\bar{\alpha_t}}\epsilon, \quad where \; \epsilon \, \sim N(0,I) $$
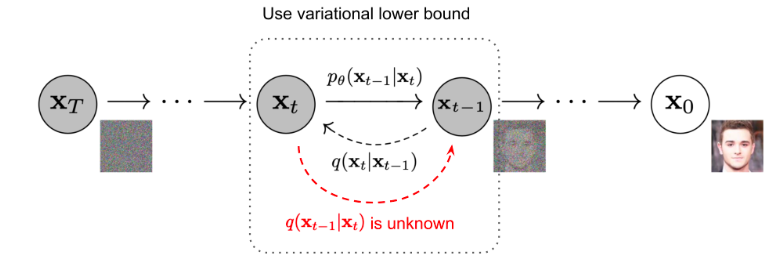
- reverse : Gaussian noise $x_T$ 에서 denoising 하면서 이미지 $x_0$ 를 만드는 과정 위 과정을 그대로 reverse 하는건( $q(x_{t-1}|x_t)$ ) 어려우니까 parameterized Gaussian transitions 을 이용. $p_\theta$
reverse diffusion 을 의미
$$ p_\theta\left(\mathbf{x}{0: T}\right):=p\left(\mathbf{x}T\right) \prod{t=1}^T p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right), \\ p\theta\left(\mathbf{x}{t-1} \mid \mathbf{x}t\right):=\mathcal{N}\left(\mathbf{x}{t-1} ; \mu_\theta\left(\mathbf{x}t, t\right), \mathbf{\Sigma}\theta\left(\mathbf{x}_t, t\right)\right) $$
$$ where \quad \boldsymbol{\mu}_\theta\left(\boldsymbol{x}_t, t\right):=\frac{1}{\sqrt{\alpha_t}}\left(\boldsymbol{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}t}} \boldsymbol{\epsilon}\theta\left(\boldsymbol{x}_t, t\right)\right) $$
$\boldsymbol{\epsilon}_\theta\left(\boldsymbol{x}_t, t\right)$ : 아래 방식으로 optimizing 하는 diffusion model
- optimization
$$ \min \theta L(\theta), \quad \text { where } \quad L(\theta):=\mathbb{E}{t, \boldsymbol{x}0, \boldsymbol{\epsilon}}\left[\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}\theta\left(\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)\right\|^2\right] \text {. } $$
- plugging learned score function
$$ \boldsymbol{x}{t-1}=\boldsymbol{\mu}\theta\left(\boldsymbol{x}_t, t\right)+\sigma_t \boldsymbol{\epsilon}=\frac{1}{\sqrt{\alpha_t}}\left(\boldsymbol{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}t}} \boldsymbol{\epsilon}\theta\left(\boldsymbol{x}_t, t\right)\right)+\sigma_t \boldsymbol{\epsilon} $$
conditional diffusion model 을 쓰는 image translation 에서는 $\epsilon_\theta$ 이 $\boldsymbol{\epsilon}_\theta\left(\boldsymbol{y}, \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)$ 로 대체된다. $\boldsymbol{y}$ : 상응하는 타겟 이미지
MCG(Manifold Constrained gradient)
$x_{src}$ : source image, $x_{trg}$ : target image
$d_{src}$ : source text , $d_{trg}$ : target text
$$ \text{total loss of image-guided translation } : \ell_{t o t a l}\left(\boldsymbol{x} ; \boldsymbol{x}{t r g}, \boldsymbol{x}{s r c}\right), \quad \\ \text{total loss of text-guided translation } : \ell_{t o t a l}\left(\boldsymbol{x} ; \boldsymbol{d}{t r g}, \boldsymbol{x}{s r c}, \boldsymbol{d}_{s r c}\right) $$
MCG 이용해서 reverse diffusion 으로 샘플링한 것
'2023 Summer Session > CV Team 2' 카테고리의 다른 글
| [7주차/백서경/코드리뷰] ViTPose (0) | 2023.08.21 |
|---|---|
| [7주차 / 임종우 / 논문리뷰] ViTPose: Simple Vision Transformer Baselines for Human Pose Estimation (0) | 2023.08.19 |
| [7주차 / 박민규 / 논문리뷰] Big Transfer : General Visual Representation Learning (0) | 2023.08.17 |
| [6주차 / 박민규 / 논문리뷰 ] ViTAE (0) | 2023.08.17 |
| [6주차 / 김지윤 / 논문리뷰] ViTAE : Vision Transformer Advanced by Exploring Intrinsic Inductive Bias (0) | 2023.08.11 |





댓글 영역