[6주차/장수혁/논문리뷰] SCORE-BASED GENERATIVE MODELING THROUGH STOCHASTIC DIFFERENTIAL EQUATIONS

해당 포스팅은 5주차 포스팅에 이어 DDPM과 NCSN이 모두 Score-based generative modeling이고, 이 2개의 모델을 Stochastic Differential Equations (SDE) 하에서 일반화할 수 있다는 것을 소개해주기 위해 작성되었습니다.

---

Abstract

Noise로부터 data를 만들어 내는 것은 generative modeling이다. 저자들은 노이즈를 천천히 주입함으로써 complex data distribution을 known prior distribution으로 만드는 SDE 방식을 소개한다.  노이즈를 제거해서 다시 data distribution으로 돌아가는 과정은 reverse SDE이다.

 

여기서 reverse SDE는 perturbed data distribution의 score에만 의존한다! 즉 pdf의 그래디언트 성분을 여기서도 주요하게 사용한다. 이 Score는 neural network를 활용해 추정이 가능하며, numerical SDE solver를 이용해 sampling을 진행한다

SDE framework는 기존의 score-based generative model, diffusion probabilistic model을 통합하고 새로운 sampling procedure와 modeling capabilities를 열어주었다

• Predictor-Corrector Framework : Discretized reverse-time SDE에서 발생한 error 교정
• Equivalent neural ODE : SDE와 동일한 distribution에서 sampling 진행하지만, 정확한 likelihood computation이 가능하고, sampling efficiency가 좋음 (SDE의 deterministic version)

 

결국, score-based generative model로도 처음으로 high fidelity의 1024 x 1024 image를 생성하는데 성공하였다.

 

---

SMLD & DDPM : Recap

 

Score-based generative model을 하나로 통합한 SDE framework를 알아보기 전에 SMLD와 DDPM에 대해 간단히 짚고 넘어가보자.

우선 논문에서는 SMLD라는 용어가 나오는데 Denosing score matching with Langevin Dynamics의 약자이다. 이전 포스팅에서 다룬 NCSN과 동일한 것이다. NCSN은 애초에 loss가 score network의 output과 x로부터 noise x를 만들어내는 근사된 분포에서 실제 계산한 score값을 최소화하는 과정이기 때문에 당연히 score-based generative model이다.

좌측 항 : Score Estimator(Neural Network), 우측 항 : 노이즈 x를 생성하는 근사 분포에 대해 실제 계산한 Score 값

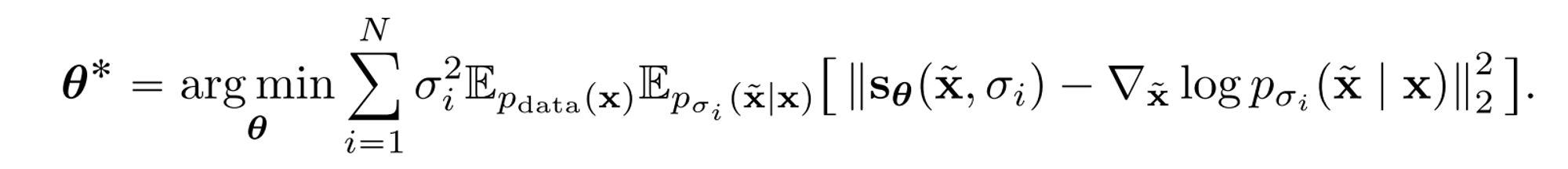
실제 sampling은 gradient ascent 과정으로 아래와 같이 진행된다.

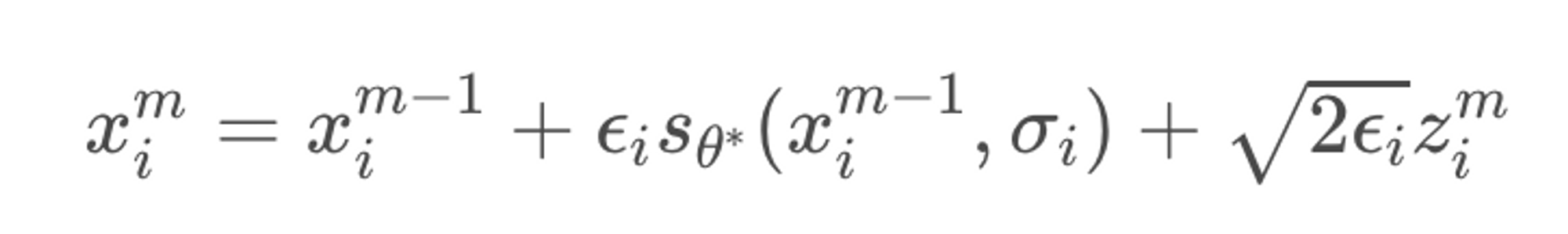
Local maxima에 빠지지 않기 위해 random noise z가 더해지고, 모든 데이터 공간에서 정확한 score 추정을 위해 데이터 분포 자체에 노이즈가 σ만큼 들어가 Noise conditional 환경을 만들어준다.

 

 

DDPM의 forward 과정에서는 noise scale을 단계적으로 증가시킨 β를 사전에 정의하고 원본 데이터를 파괴시켜나간다.

N이 커질수록 Noise scale은 커진다

각 data point에 대해 perturbation kernel을 Markov Property (미래 시점은 현재에만 영향, 과거 시점은 영향 X)에 따라 다음과 같이 정의할 수 있다. Time step별 forward / backward는 가우시안 분포를 따른다고 이미 증명되어 있고, 노이즈가 더해지는 각 process에서 변수의 variance는 1로 고정된다.

왼쪽의 식은 이미 사전에 정의된 βi에 맞춰 가우시안 분포 만들어진 것 / 오른쪽 식은 왼쪽의 식을 연속적으로 reparametrization하면 유도됨

 

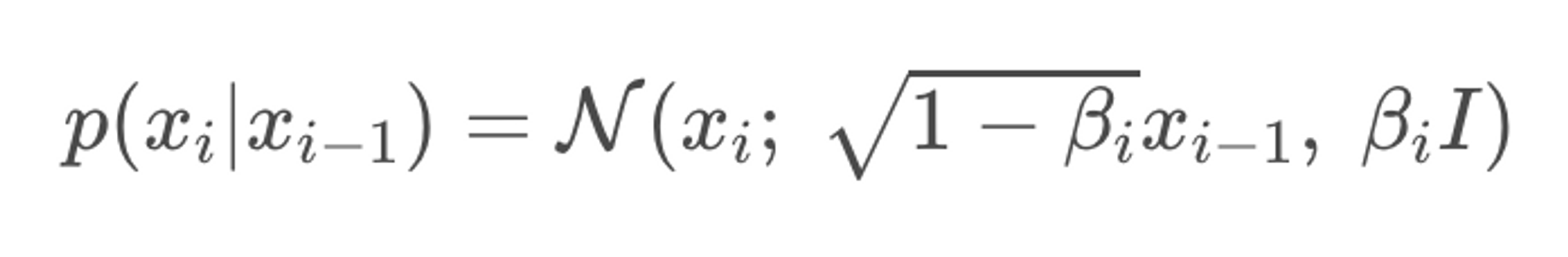
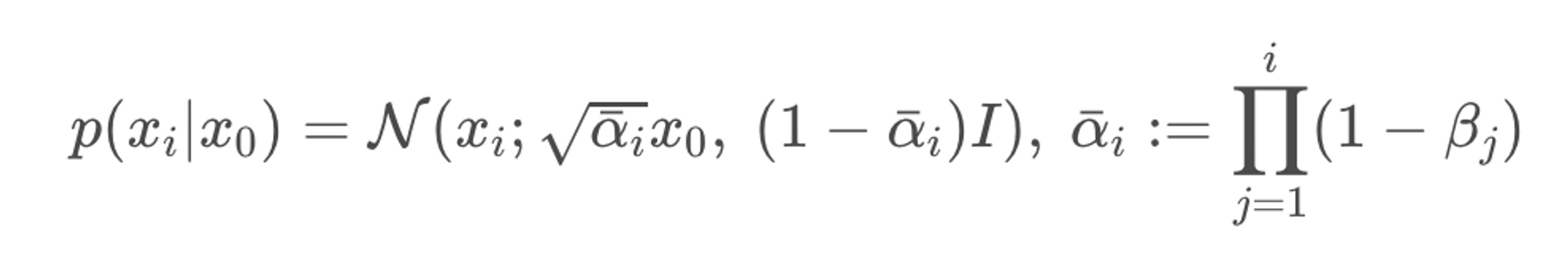
우측의 식은 아래와 같이 perturbed data distribution으로도 표현할 수 있다.

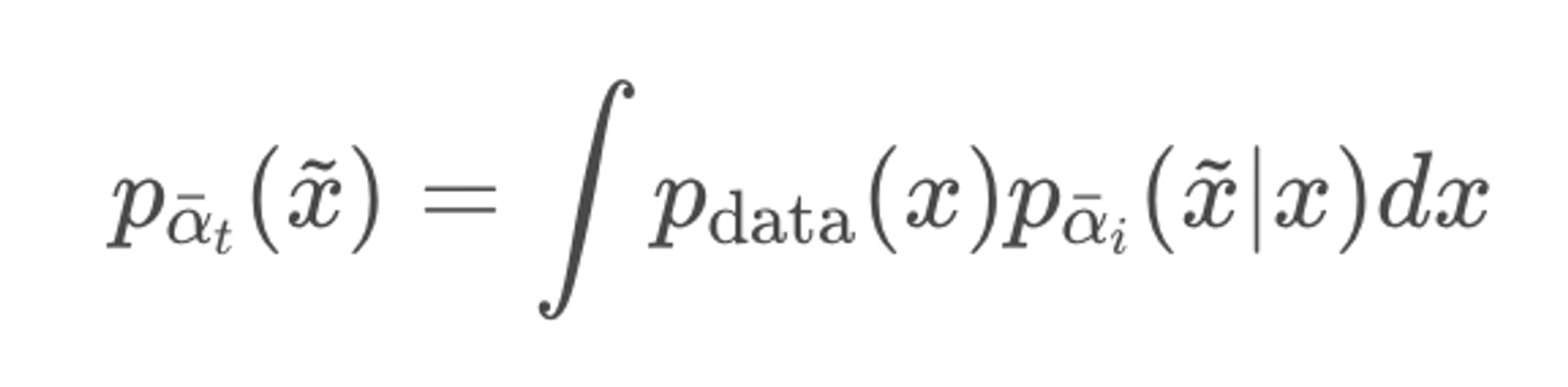
Reverse process의 경우 논문에서는 노이즈인 입실론을 추정하는 것이 핵심이었기 때문에 얼핏보면 score-based 형태가 아닌 것처럼 보인다.

기존 DDPM sampling method

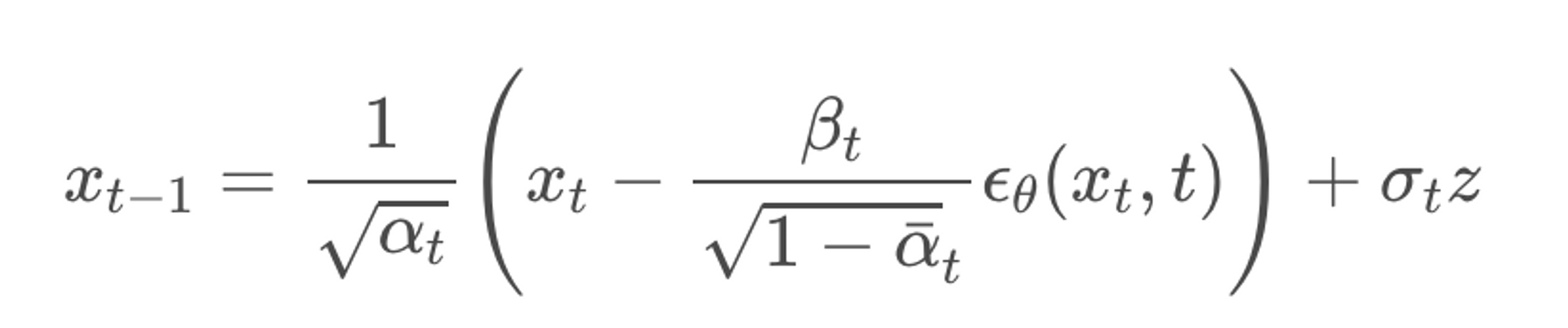
하지만 만약 SMLD처럼  score matching 형태로 reverse process를 표현하면 아래와 같다. DDPM의 denoising을 SMLD의 gradient ascent과정으로 치환했다고 생각하면 된다. NCSN에서 noise의 크기가 update 계수로 붙었기 때문에 아래에서도 동일하게 β가 붙는 모습이다.

DDPM reverse processs를 score-based로 표현한 모습

 

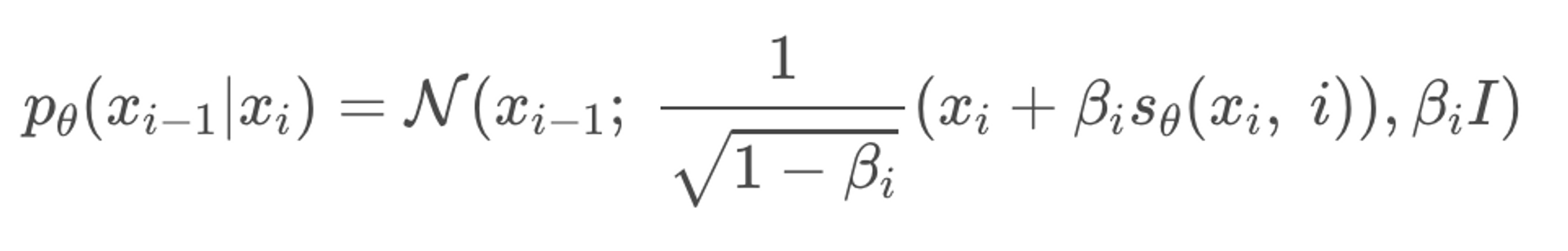
위의 score function은 아래의 loss에 따라 학습이 된다. SMLD와 매우 유사함을 알 수 있다. P(noise x|x)를 DDPM에서의 P(x(t)|x(0))라고 생각하면 된다. 또한 계수가 1−α로 P(x(t)|x(0))의 variance인데 SMLD의 loss 계수도 P(noise x|x)의 variance인 σ^2이었다.

 

 

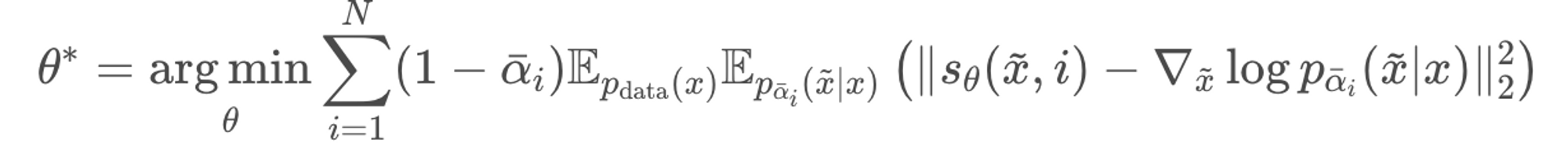
그렇게해서 loss term을 만족하는 θ에 대하여 sampling을 진행하면 아래와 같은 수식이 나온다. 이를 Ancestral sampling이라 한다. (Score-based DDPM sampling 방식)

 

 

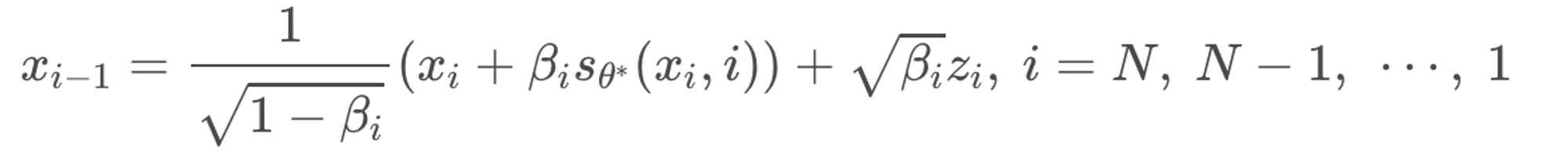
결론적으로 DDPM과 SMLD 모두 score-based generative model임을 확인할 수 있다.

 

 

 

 

 

---

Solving SDE

Solving reverse-time SDE -> Score-based generative model

 

논문의 핵심은 이러한 score-based generative model들을 Stochastic Differential Equations (SDE)를 통해 단일화된 framework를 구축해 일반화할 수 있다는 것이다.

 

지금까지는 유한한 숫자에 한해, 이산적으로 data에 noise를 첨가하여 점점 data를 perturbing시켰다. 만약, data가 noise로 변해가는 과정이 일련의 연속 시간에 대해 정의될 수 있다면 이를 확률 미분 방정식(SDE)으로 모델링할 수 있다고 한다. 이를 아래와 같은 식으로 나타낼 수 있다.

Forward SDE

 

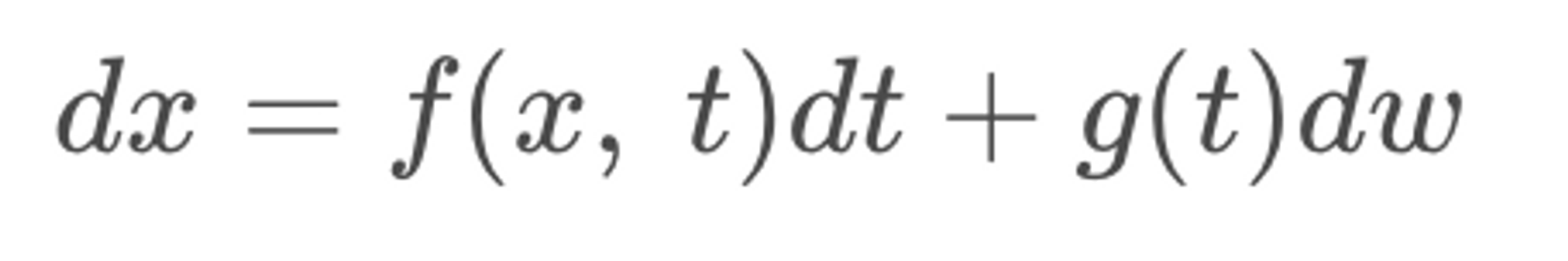
먼저, SDE의 개념에 대해 알아보도록 하자.

SDE는 상미분방정식(ODE)에 randomness가 추가된 미분 방정식이다.

ODE란 독립 변수가 하나인 미분방정식을 말한다.

미분방정식은 미지의 함수와 그 도함수, 그리고 함수값에 관계된 여러 변수들에 대한 방정식을 의미한다.

 

Forward SDE 수식에서 dx = f(x,t)dt 부분만 떼보면, x라는 함수가 t라는 하나의 독립 변수만을 가지고 있는 ODE라고 생각할 수 있다.

ODE를 푼다는 것은 식을 만족하는 해를 찾는 것이며 그것은 어떤 함수가 이 방정식을 만족하는가와 같다. 여기서는 x(t)를 찾는 것이다.

하나의 예시를 보면 다음과 같다

[고려대학교 Open DMQA Seminar] Score-based Generatvie Models and Diffusion Models 발췌

 

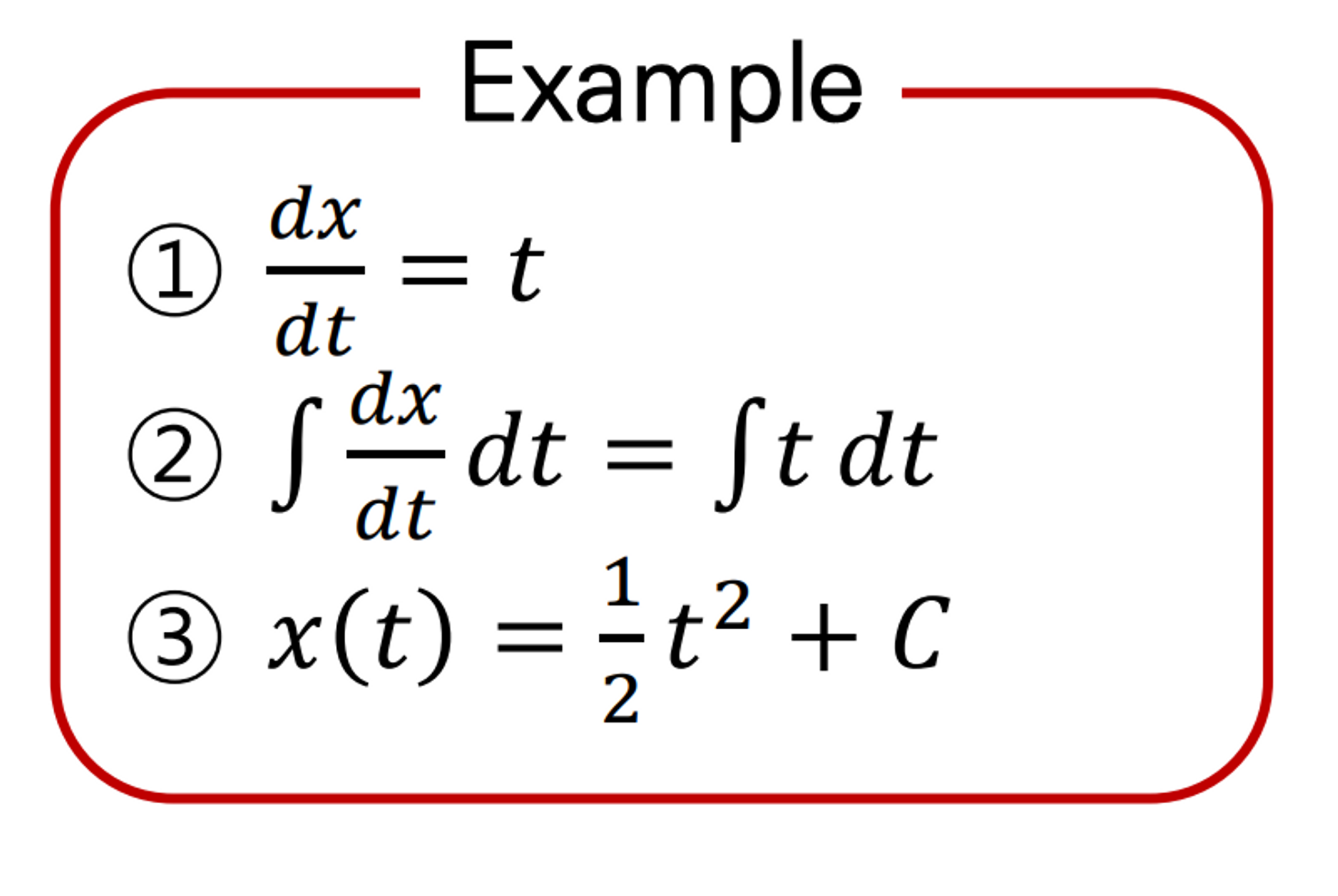
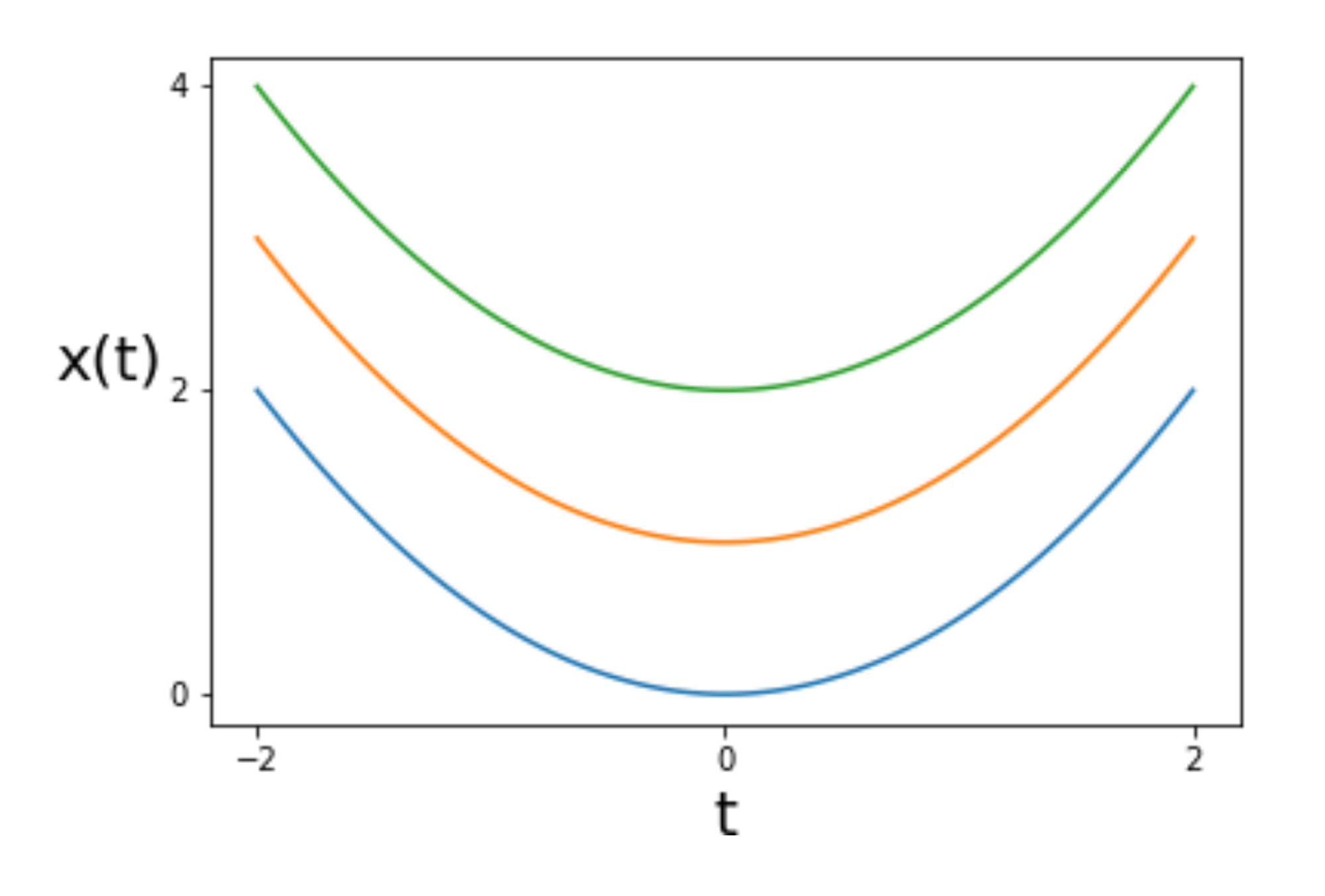
SDE는 한발 더 나아가 dx = f(x,t)dt 에 g(t)dw라는 것이 추가되었다. g(t)dw는 randomness기 때문에 이제 더 이상 f(x,t)가 모든 t에 대해 하나의 식으로 정의되지 않고 Random process가 되어버린다. 이를 아래처럼 t 시점으로 짤라서 보면 특정 t에 대해 x(t)의 확률분포를 확인할 수 있다.

[고려대학교 Open DMQA Seminar] Score-based Generatvie Models and Diffusion Models 발췌

 

위에서 설명한 내용을 좀더 직관적으로 설명해보면, 확률 미분 방정식의 해는 해당 변화율 (dx, dt, dw)이 그리는 궤도 = solution x(t)로 이해할 수 있다. (단, 이해를 돕기 위해 dw의 영향은 제외하자)

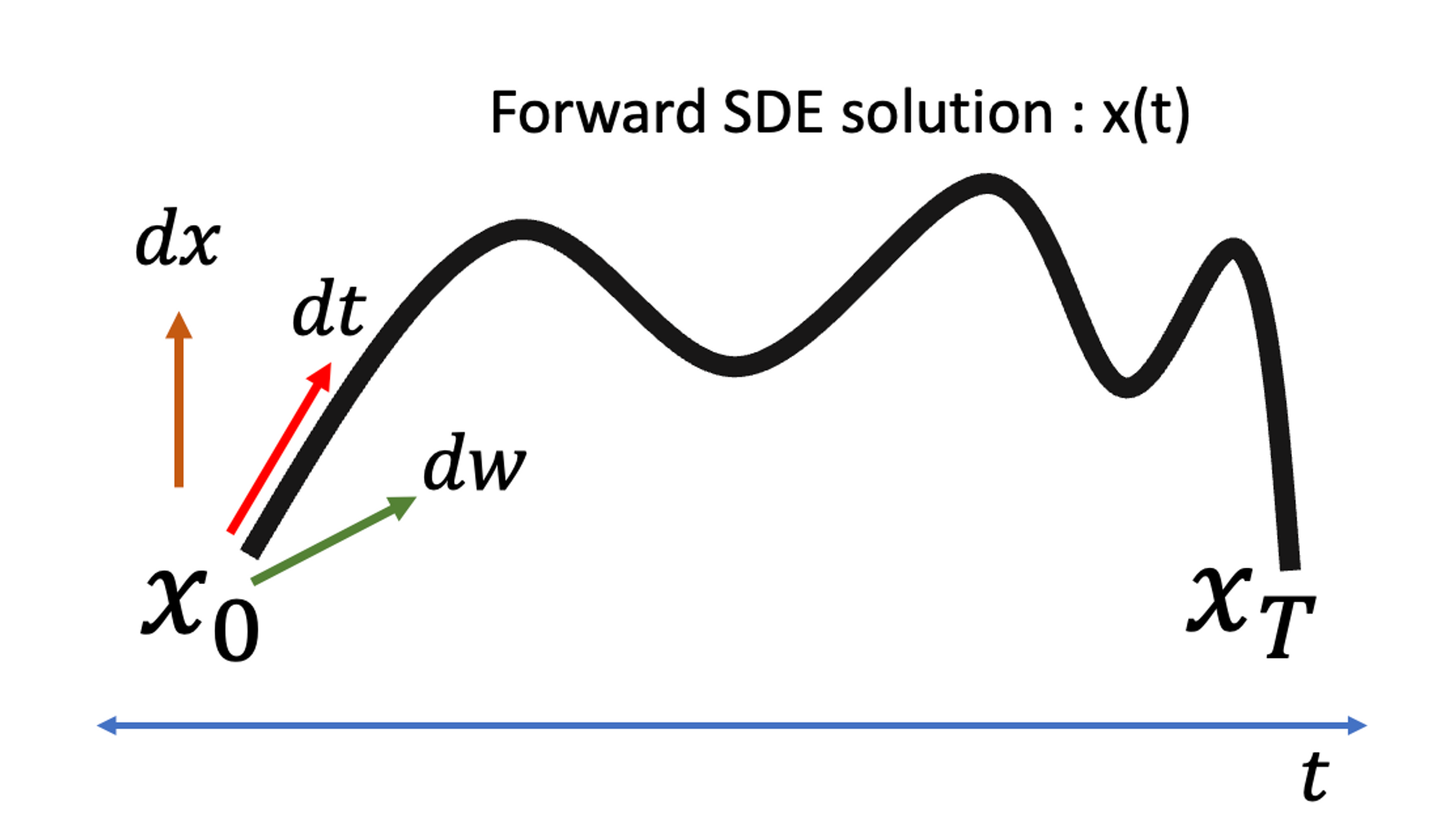
dw는 t에만 의존하는 diffusion term이라 x(t)가 그리는 궤도와는 무관하고, drift term인 dt만이 x의 실제 궤도를 따라가는 방향을 정의한다. 결국 solution x(t)는 특정 시점 t가 주어졌을 때, 해당 위치에서의 x(t)를 찾을 수 있는 함수의 꼴로 정의되고, 이를 나타낸 것이 위의 그림이다.

 

그런데 생각해보면, 꼭 x(0)에서 x(T)로 일방향적으로 가라는 법은 없다. dt의 계수가 현재와 반대방향으로 정의된다면 x(T)에서 x(0)을 따라가면서 x(t)를 예측하는 새로운 문제를 정의할 수 있다.

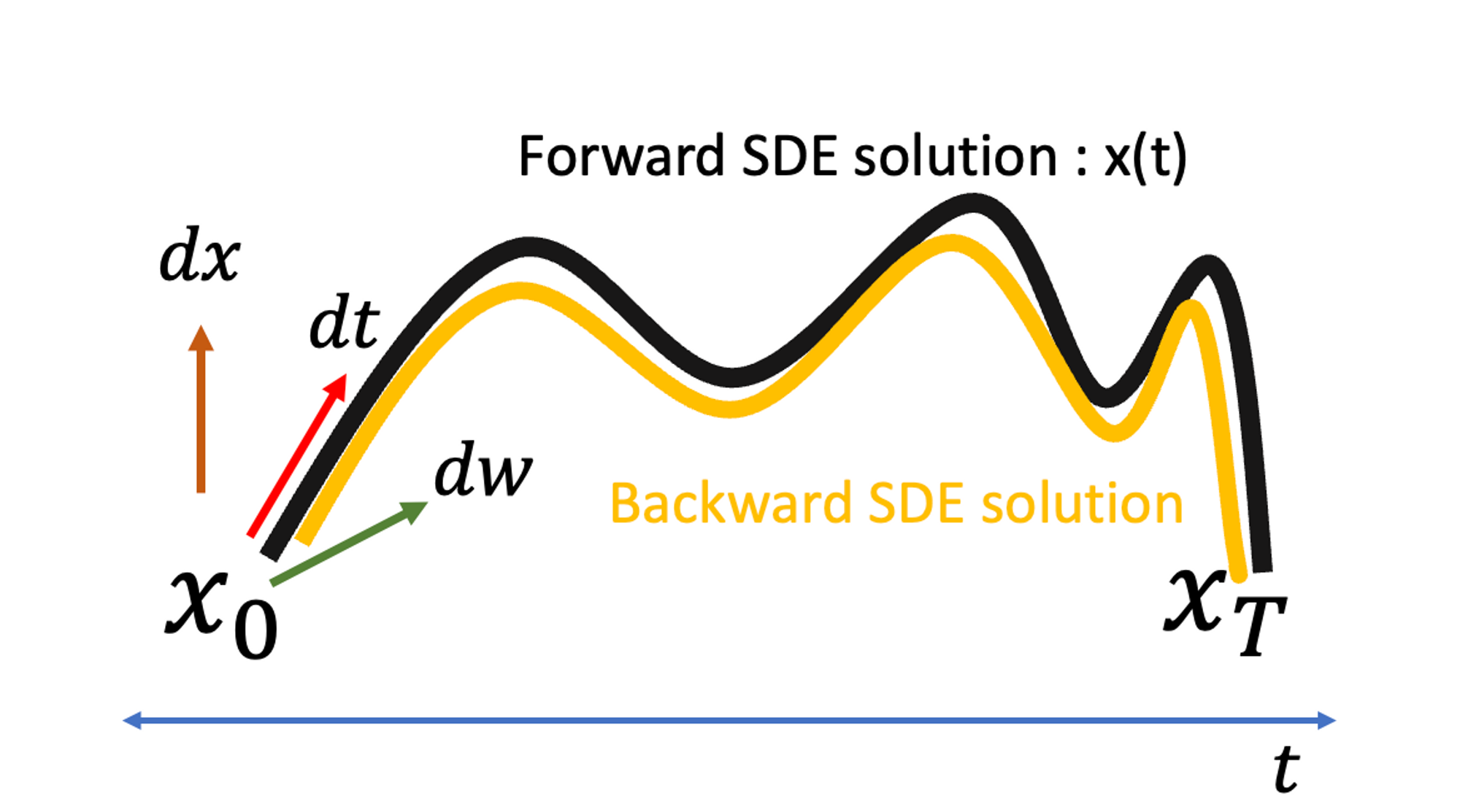
Backward(or Reverse) SDE의 식은 아래와 같은데, g(t)dw는 forward와 동일하고 이는 여전히 x(t)의 궤도와는 무관하다. 다만, Drift term인 dt가 적용되는 궤도 방향이 반대가 되야하므로 익숙하게 봐왔던 score term이 들어가는 것을 확인할 수 있다.

Backward SDE

 

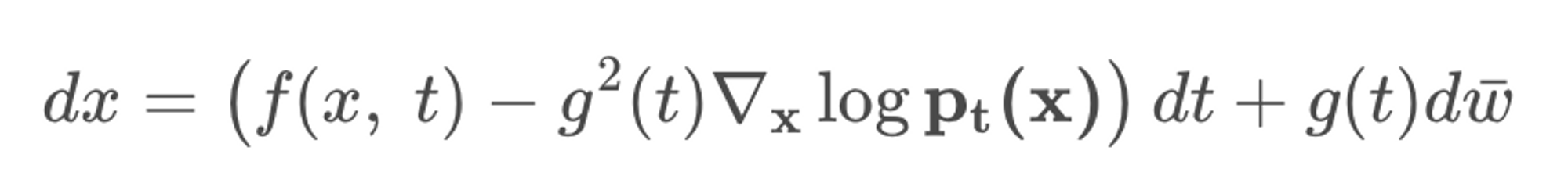
결론적으로, Forward SDE와 Backward SDE는 출발점과 도착점이 다르지만 서로 같은 궤도 x(t)를 그려야 한다.

이 말은 우리가 Forward SDE를 미리 알고 있다면 Backward SDE에게 솔루션을 제공할 수 있다는 것이다.

 

뿐만 아니라, score term을 예측하는 것은 곧 Backward SDE를 푸는 것이며 이는 sampling으로 이어지므로 SDE solver 형태의 모든 샘플러가 생성에 관여할 수 있다는 일반화가 가능해진다.

 

 

---

Extension of Diffusion

Overview of score-based generative modeling through SDEs

 

Diffusion 모델링의 기본은 특정 데이터 분포(P0(x))를 따르는 x(0)에서 가우시안 노이즈에 가까운 perturbed data인 x(T)를 만드는 것이다.  여기서 x(T)는 Pt(x)라는 prior 분포를 따른다고 한다.

 

앞서 간략히 소개한 Forward SDE가 이 기본 diffusion process를 모델링한것이라고 할 수 있다. 여기서 f(x,t)는 vector function으로 x(t)의 drift coefficient이고, g(t)는 scalar function으로 x(t)의 diffusion coeffcient이다. g(t)는 scalar라 x와는 독립이다.

Drift coefficient : f(x,t) / Diffusion coefficient : g(t)

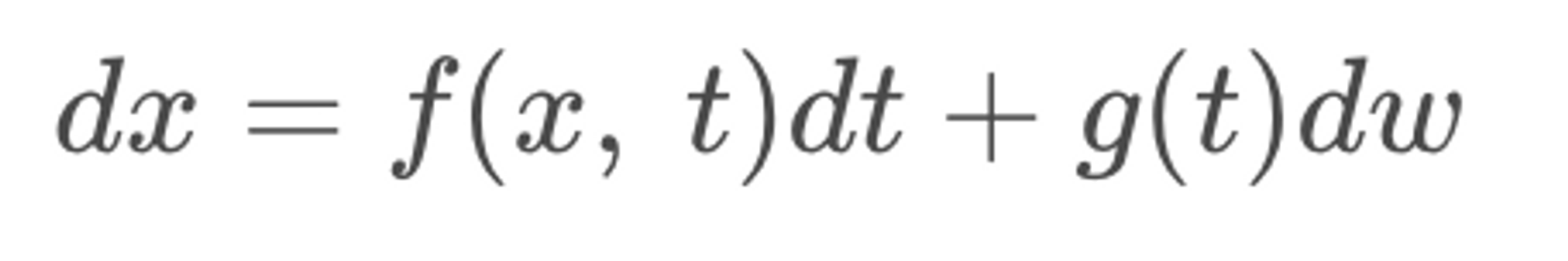
Forward SDE는 coefficients들이 state와 time에 대해 모두 Lipshitz 정리를 만족한다는 가정 하에 (미분 값이 bounded되어 있다고 할 때) 한정된 변화율 사이에서 unique strong solution을 가질 수 있다고 한다. (상세 내용은 범위를 초과하여 생략하오니, 논문을 참고해주기 바란다)

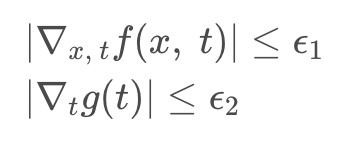
Backward SDE도 마찬가지로 다시 살펴보면, prior 분포를 따르는 x(T)에서 원본 데이터 분포를 따르는 x(0)으로 가는 과정이다.

Prior분포를 가우시안으로 정의했다면 sampling을 통해 x(T)를 구할 수 있고, 아래의 process를 통해 x(0) 또한 얻을 수 있는데 Forward SDE의 역과정이 SDE임은 오래전에 증명되었다고 한다.

 

Backward SDE

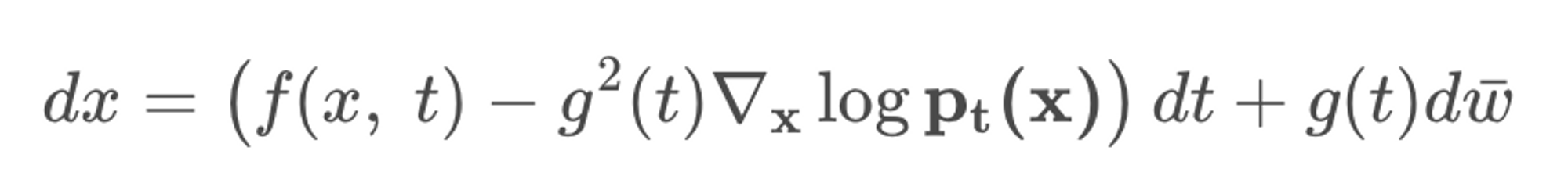
여기서 w_bar는 표현만 다를뿐 Forward SDE에서의 w와 의미가 동일하다. 위의 식에서 만약 모든 t에 대해 Pt(x) 분포의 score값을 알 수 있다면, 우리는 x(T)로부터 x(0)를 샘플링 할 수 있게 된다.

 

그렇다면 그 score는 어떻게 알 수 있다는 말인가? 사실 Pt(x)분포는 우리가 알 수 있는 방법이 없기 때문에 score matching을 이용한 score-based neural network를 학습시켜 score를 추정한다. 그것이 앞서 본 DDPM 및 SMLD의 방식이다. 다만 여기서 다른 점은 이산 변수가 아니라 연속 변수 t를 쓴다는 것이다.

 

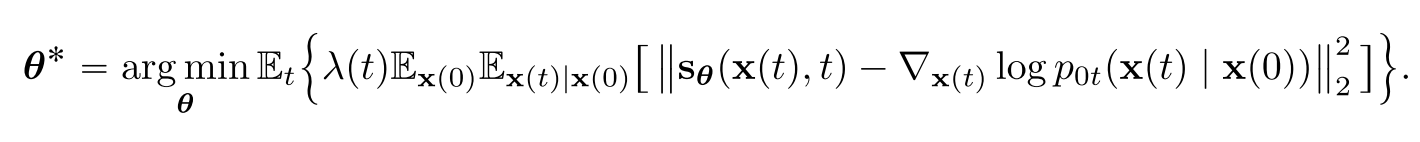
DDPM과 SMLD의 discretized한 process도 continuous하게 확장해보자.

 

SMLD에서는 각 스텝에서의 노이즈 분포 q(noise x|x)가 N(noise x|x, σ^2 I)를 따르기 때문에  forward process를 Markov chain에 기반해 나타낸다면 아래와 같이 나타낼 수 있다.

 

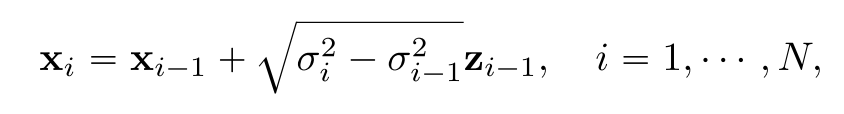
해당 식에서 N이 극한으로 증가한다면, noise scale은 연속 시간에 대한 함수로 표현이 가능하고 i를 더이상 쓰지 않고 모두 t로 바꿀 수 있다.

이때의 Markov chain을 continuous한 x(t)로만 바꾼다면, 델타가 매우 작다는 가정 하에 테일러 1차 근사를 활용해 미분 방정식으로 근사할 수 있다.

 

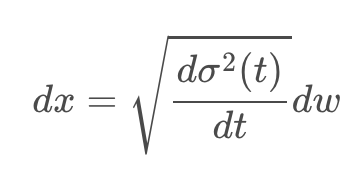
마찬가지로 DDPM 또한 원래 forward process가 아래의 좌측 사진과 같다. 여기서도 N을 무한으로 보내버린다면, 아래의 오른쪽과 같은 형태가 된다. β의 경우 원래 scheduling된 각 Markov process의 노이즈이기 때문에 미소 단위의 variance 변화에 대해 delta가 추가로 한번 곱해지는 형태가 된다.

 

 

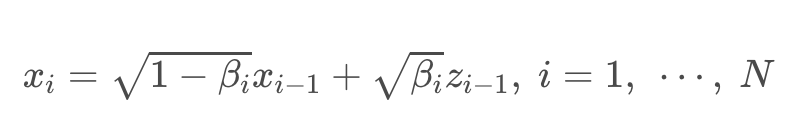
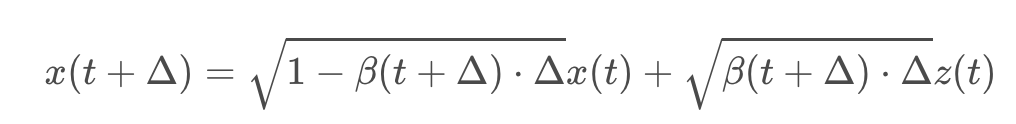
그리고 이를 위와 같이 테일러 1차 근사를 활용해 미분 방정식으로 근사하면 아래와 같은 식으로 정리할 수 있다.

논문에서는 SMLD의 미분 방정식을 variance가 계속 증가하는 VE(Variance Exploding) SDE이고, DDPM의 미분 방정식은 variance가 유지되는 VP(Variance Preserving) SDE라고 명명하였다. 

 

VP SDE의 형태에서 영감을 받아 저자들은 새로운 sub-VP라는 SDE 형태를 만들어냈는데, likelihood 측면에서 좋은 성과를 냈다고 한다. 다소 난해한 수학적 증명이 들어가, 이 부분에 대한 설명은 생략한다. 

 

중요한 것은 sub-VP SDE는 VP SDE를 upper bound로 가진다는 것이다. (1-exp() 부분이 1보다 클 수 없으므로)

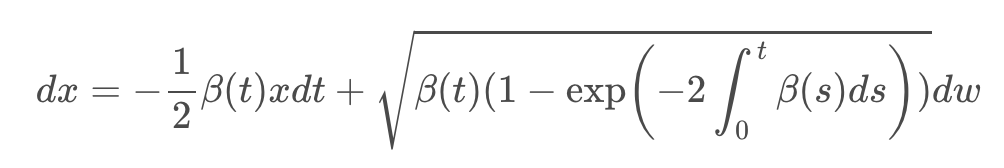
결론적으로 앞에서 만든 미분방정식들은 모두 Forward SDE 인 dx = f(x,t)dt + g(t)dw 형태의 수식을 따라간다고 볼 수 있다.
(VE,VP,sub-VP SDE는 general SDE의 special cases)

 

Reverse SDE도 마찬가지로 앞서 Forward SDE에서 구한 f(x,t)와 g(t)를 바탕으로 generic하게 정의한 Reverse SDE 수식에 대입하면 된다. 아래는 Reverse-VP SDE의 예시이다.  결국 나머지는 다 Forward SDE에서 주어지고, score function의 값만 학습을 통해 얻어내면 된다.

 

 

 

 

 

 

 

---

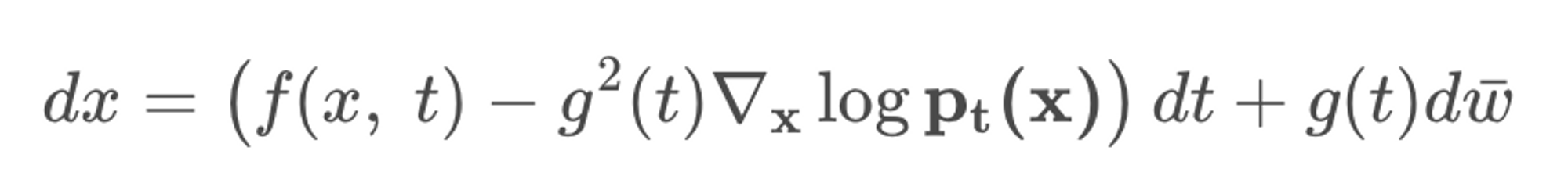
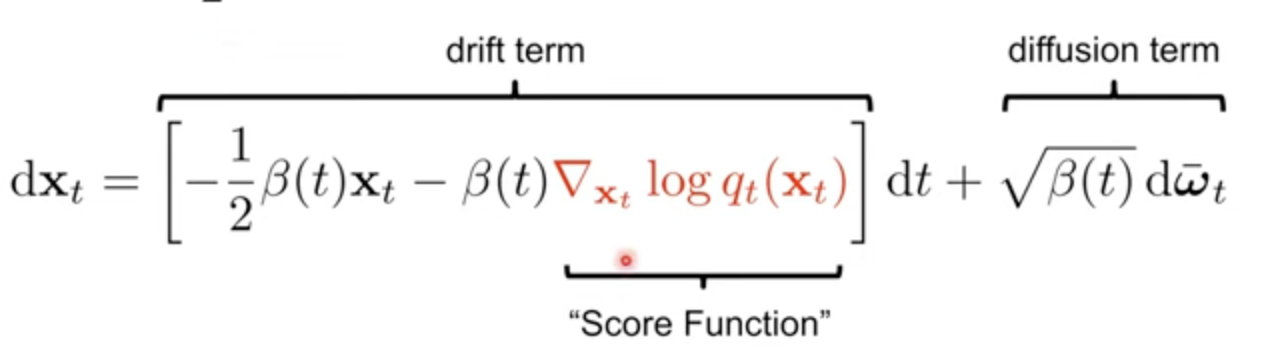
Predictor-Corrector Samplers 

일반적으로 이렇게 SDE를 풀어내는 것은, Forward이후 Backward 때 score prediction만 진행하게 되는 과정인데, 

저자들은 추가로 MCMC approach를 적용한다 (NCSN에서의 Langevin dynamics). 

 

간단하게 step을 정리하자면 다음과 같이 나타낼 수 있다.

1. Numerical SDE가 다음 time step의 (시점은 이전 시점) solution을 예측한다  (Numerical SDE = Predictor)

2. 해당 Point에서 score estimation을 토대로 correction sampling(조정 작업)을 진행한다. (Score model = Corrector)

---

Probability Flow and Neural ODE

논문의 저자들은 추가적으로 모든 diffusion process에 대하여 궤적이 SDE와 같은 주변 확률 밀도 Pt(x)를 공유하는 deterministic한 process가 존재한다는 것을 밝혔다. 

 

아래가 우리가 아닌 일반적인 Reverse SDE라면 

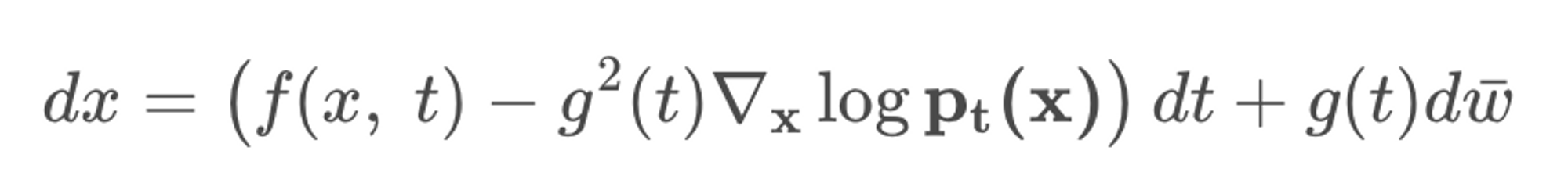
아래의 수식은 여기에서 randomness를 제거한 ODE이다. 이것을 저자들은 probability flow ODE라고 명명했다.

그리고 해당 ODE는 SDE에서 score값이 구해져야만 결정이되고, score는 neural network로 예측되기 때문에 Neural ODE의 예시라고도 한다. 

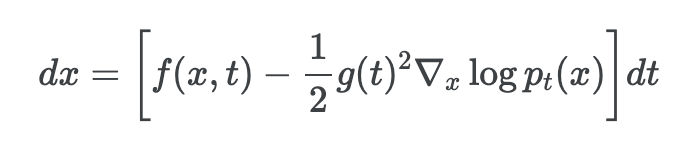
Probabillity flow ODE를 이용하면 randomness가 제거되었기에 어떠한 데이터가 들어와도 exact likelihood computation이 가능하고 효율적인 sampling이 가능하다고 한다.

 

해당 논문은 Score-based generative modeling에 대한 Generic한 Framework를 SDE위에서 구축했다는 엄청난 contribution이 존재한다. 기본적인 Diffusion model의 종류인 DDPM과 NCSN 논문보다도 방대하고도 깊은 수식때문에 정말 어려운 논문이었고, 상세한 의미를 해석하지는 못하였다. 그럼에도 불구하고 diffusion과 score-based generative model에 관심있는 독자들이 이를 통해 조금이나마 도움을 얻었으면 하는 바람이다.

---

Reference

https://kimjy99.github.io/%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0/sbgm/

[논문리뷰] Score-Based Generative Modeling through Stochastic Differential Equations

https://junia3.github.io/blog/scoresde

Welcome to JunYoung's blog | Score-based generative modeling through stochastic differential equations 이해하기

https://www.youtube.com/watch?v=uFoGaIVHfoE&t=3669s