[5주차/임청수/논문리뷰] Denoising Diffusion Probabilistic Model
작성자 : 17기 임청수
0. Diffusion Overview
- Diffusion model은 backward process를 통해서 explicit(가우시안)한 분포에서 sampling한 random noise로부터 denoising을 통해 데이터를 만들어내는 생성 방식.
- Forward process(=diffusion process)와 backward process(denoising)으로 구성.
- 이미지에 noise를 주입하는 forward process는 쉽게 정의할 수 있지만, backward process는 정의하기 어려움. 따라서
- DDPM은 backward process를 diffusion probabilistic model로 학습하는 것을 의미함.

- 위 그림에서 q는 noise를 더하는 forward process(=diffusion process)이고,
- P는 gaussian noise를 원래 이미지로 되돌리는 reverse process를 나타냄.
1. Forward Process
- Forward process q는 미세한 Gaussian noise를 원본 이미지 에 점차적으로 추가하는 과정을 의미함.
- Noise를 주입하고 제거하는 과정은 큰 변화이기 때문에 한번에 적용하기 어려움. 따라서 T=1000 step으로 변화를 매우 작게 하여 학습을 쉽게 만듦. 이때 Markov Chain으로 표현됨.
1. Markov Chain
정의 : Markov 성질을 갖는 이산 확률과정
Markov 성질 : 특정 상태의 확률(t+1)은 오직 현재t)의 상태에 의존한다. 이산 확률과정 : 이산적인 시간(0초, 1초, 2초 ...) 속에서의 확률적인 현상
0시점에서 T시점으로 noise를 주입하고 제거하는 과정에서 1000번의 step으로 나누어 수행하고 이때 Markov chain을 적용

- Gaussian noise를 서서히 주입하는 과정
- Forward process는 조건부 가우시안 의 Markov chain으로 구성됨.


- 주입되는 gaussian noise의 크기는 사전에 정의되고. 로 표현됨.
- 따라서 Forward process는 따로 학습할 필요가 없음.

2. Backward Process
- Noise로부터 이미지를 복원하는 과정.
- q와 반대로 noise를 점진적으로 걷어내는 denoising process를 의미함.
- 따라서 조건부 확률 q와 time이 반대로 뒤바뀐 p로 표현됨.

- 사전에 정의된 q와는 달리 p는 알기 어렵기 때문에 p_theta로 근사하여 구하고 p_theta는 학습된 모델을 통해 구함.

위 식에서 평균과 표준편차는 학습되어야 하는 parameter임.
3. Diffusion Objective Function
- Maximize log likelihood
DDPM은 Loss를 굉장히 간단하게 정의하여 성능을 개선함.

4. DDPM Loss
- L_T는 p가 generate하는 noise와 q가 가 주어졌을 때 generate하는 T시점의 noise간의 분포 차이
- DDPM에서는 beta를 학습 가능한 파라미터가 아니라 사전에 정의한 상수로 fix하기 때문에 고려하지 않아도 됨
- 이유
1000 step으로 나누고 noise를 linear하게 증가시키도록 linear noise scheduling을 설정할 경우 최종적인 X_T는 isotropic gaussian(원형 대칭) 분포와 매우 유사하게 형성되기 떄문에 굳이 학습 필요 X

- L_(t-1)는 p와 q의 reverse / forward process의 분포 차이를 의미함. Forward대로 Denoising하기 때문에 두 값이 최대한 비 슷해지는 방향으로 학습을 진행. 총 4가지에 대해서 최적화 진행
(1) 표준편차의 상수화
- P의 표준편차는 상수 행렬에 대응함. 따라서 학습 대상이 하나 줄어듦.

(2) q(x_(t-1)|x_t, x_0)
앞서 정의한 것처럼 표현할 수 있음

(3) p_theta(x_(t-1)|x_t)

(4) 평균(x_t,t)
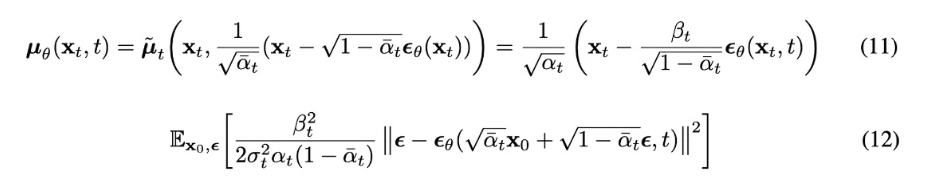
(5) sampling

(6) L_(t-1) 정리

(7) L_simple(theta)
Loss function을 epsilon에 대한 식의 형태로 다시 한 번 표현할 수 있음.
이러한 형태를 simplified objective function이라 부르고 더 효율적인 학습이 가능함.


Reference
[blog] : https://process-mining.tistory.com/188
[Youtube] : https://www.youtube.com/watch?v=_JQSMhqXw-4
[paper] : https://arxiv.org/abs/2006.11239
