고정 헤더 영역
상세 컨텐츠
본문
LONG SHORT TERM MEMORY
# ABSTRACT
기존 vanilla RNN은 Time Interval이 긴 데이터 정보 저장의 한계점이 있었고 이는 주로 Error back propagation (역전파과정)에서 기울기 소실이 발생하기 때문이었다.
이에 본 논문은 이를 해결할 수 있는 efficient-gradient-based model인 LSTM을 제안한다.
LSTM에서는 특정 정보가 Gradient에 약 1000번의 time step 이상의 interval에도 정보를 소실하지 않고 효과적으로 정보를 전달할 수 있다.
후반부에서는 인위적으로 만들어낸 다양한 패턴들에 대해서 LSTM을 적용시켜 RTRL, BPTT, Recurrent Cascade-Correlation, Elman nets, Neural Sequence Chnking등과 비교해보았으며, 실험을 통해 LSTM의 우수함을 입증하고 있다. 그 결과 LSTM은 단순히 성능 지표만 높을 뿐 아니라, 기존 RNN류 모델들이 풀지 못했던 Long Time Lag Task에서 최초로 성공을 거두었다고 언급한다.
+) RNN(Recurrent Neural Network) 개념 및 한계점 부가 설명
RNN(Recurrent Neural Network)
: 현재 step 출력이 다음 step 입력으로 순환됨 → 순환신경망

RNN 구조 문제점
-Long time step에 대해서 학습이 이루어지지 않음 (time step이 10 이상인 경우 성능 저하 발생)
-이는 Vanishing Gradient or Exploding Gradient 로 인해 나타남 (BPTT 활용으로 인함)
(1) Long time step이 입력되면 오차 역전파시 동일 행렬곱 반복으로 인해 행렬곱 반복이 발생
W값 < 1 인 경우 Gradient Vanishing, W값 > 1 인 경우 Gradient Exploding 발생
(2) Activation function tanh을 미분해서 gradient 계산 시 1보다 작아짐
→ vanishing 확률 높아짐
# INTRODUCTION
기존의 BPTT(Back-propagation Through Time)와 RTRL(Real-Time Recurrent Learning)의 경우
기울기 소실 혹은 기울기 폭발 문제가 있으며 특히 오차 역전파 과정에서의 기울기 소실에 집중하여 특별한 유닛으로 구성된 LSTM을 해결책으로 제시한다.
+) BPTT(Back-propagation Through Time) : 시간 방향으로 펼친 신경망의 오차역전파법

한계 : 긴 시계열 데이터 학습 시 시계열 데이터의 시간 크기가 커지는 것에 비례하여 BPTT 소비자원도 커짐. 또한 시간 크기가 커지면 역전파 시 기울기가 불안정해진다.
# PREVIOUS WORK
RNN을 위한 다양한 기존 연구가 있었으나 Vanishing Gradient 문제를 근본적으로 해결하지는 못했다. 이와 관련한 다양한 연구를 본 section에서 언급하고 있다.
1) Gradient-descent variants : 학습 방법의 다양성을 주었으나 BPTT와 동일한 기울기 소실문제
2) Time-delays : short time에서만 동작
3) Time constant : LSTM과 유사한 time constant 사용했지만 fine tunning 상당 필요
4) Bengio et al.’s approach : 특정 문제에 state가 너무 많이 필요
5) Random weight Guessing : 4) 연구의 발전된 버전, 성능 더 뛰어남
CONSTANT ERROR BACKPROP(backpropagation에서의 고정적 오차)
3.1 exponentially decaying error 지수적으로 붕괴되는 error
BPTT에서의 output k에 대한 error

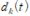
: 시간 t에서의 target 함수

: input I에서의 활성화 함수


Hochreiter의 분석은 fully connected net을 가정 unit u에서 unit v로 갈 때 q time step에 대한 error를 다음과 같은 식으로 정리하였다.


여기서 equation 2의 동그라미 친 부분이 error의 크기를 결정한다.
경우의 수 1

>1.0 for all m
곱이 q에 따라 굉장히 커지고 가중치가 진동하고 안정적이지 않은 학습이 된다.(기울기 폭발)
경우의 수 2

<1.0 for all m
곱이 q에 따라 지수적으로 감소한다. 따라서 error가 사라지고, 아무것도 학습될 수 없다.(기울기 소실)
예시

이 logistic sigmoid function면

의 최댓값은 0.25

이 0이 아닌 상수일 때

는 w값의 절댓값이 4보다 작을 때 1보다 작다.(기울기 소실)
따라서, logistic sigmoid 활성화 함수에서 error flow는 특히 초기에 가중치의 절댓값이 4보다 작을 때 사라지는 경향이 있다. 일반적으로 초기에 더 큰 가중치는 가중치의 절댓값이 무한으로 가면 함수값이 0으로 가기 때문에 도움이 되지 않는다. 마찬가지로, 학습률을 높이는 것도 큰 도움이 되지 않는다. BPTT는 이러한 부분에 민감하다. Global error flow 또한 위 식을 통해 local error flow도 함께 사라짐을 알 수 있다.
weak upper bound for scaling factor
q>1에서 equation 2는 다음과 같이 재정의할 수 있다.

여기서 W는 가중치 행렬

: outgoing weight vector
i
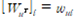
: incoming weight vector
행렬 norm을 이용하여
를 정의하고, 부등식의 성질을 이용하여 다음과 같은 부등식을 얻는다.

A – norm, e – 단위 벡터(k번째 component 제외 다 0)
이를 통해 일부 case에서 weak upper bound를 보여준다. 그러나, 만약
가 크면
의 값이 작아지는 기울기 소실 문제가 발생할 수 있다.
3.2 constant error flow : 단순 접근
- single unit
기울기 소실을 피하고 constant error flow에 도달하기 위해 local error flow 식에서

=1이 되어야 한다.

The constant error carrousel
위 식을 적분해서

식을 얻는다.
즉, f_j는 선형이어야 하고 unit j의 activation이 constant여야 한다.

실험에서
f_j=x, w_jj가 1.0일 때 보장됨을 보여줄 것이고, 이를 CEC(constant error carrousel)이라 부를 것이다. CEC는 LSTM의 중요 특징이다.
물론 unit j는 자기 자신 뿐만 아니라 다른 unit과도 연결되어 있다. 이는 2가지 큰 문제점을 가져온다.
1. Input weight conflict
total error가 unit j를 바꿈으로써 감소된다고 가정했을 때, 같은 입력 가중치는 입력값 저장 그리고 다른 요소를 무시하는데 동시에 사용되기 때문에 추가된 입력 가중치
는 weight 업데이트에서 conflict(충돌)이 발생한다. 이러한 충돌이 학습을 어렵게 만들고, 더 세밀한 메커니즘을 요구한다.
2. Output weight conflict
unit j가 이전 입력치를 저장하고 바뀌었다고 가정할 때, 단일 outgoing 가중치
에 대해 생각해보자. 같은
는 j의 내용을 저장하고 k로부터 j 내용을 유지하려 할 때 사용된다.
에서 j의 정보를 저장하고 unit k가 j에 의존하는 것을 막기 위해 conflict가 발생한다. 예시로 short time lag error가 초기 훈련 단계에서 감소되는 경우가 있는데, 이후 훈련 단계에서 long time lag error가 발생해 피할 수 없는 error가 발생한다. 이러한 conflict가 학습을 어렵게 만들고, 더 세심한 메커니즘을 요구한다.
물론, input 및 output weight conflict가 분명하게 발생하지 않을 수도 있지만, 그 효과는 긴 시간의 경우 특히 잘 나타난다. 시간이 지날수록 저장된 정보가 더 긴 기간 동안 유지되어야 할 것이며 더 많은 output들 또한 그 정보들을 더욱 더 요구할 것이다.
# 4. LONG SHORT TERM MEMORY(LSTM)
이 network는 3.2의 선형 unit j으로 구현된 CEC (Constant error carrousel*)를 확장한 것이다. 여기서 multiplicative input gate unit과 마찬가지로 multiplicative한 output gate unit이 등장하는데, input gate unit은 unit j에 저장된 정보가 다른 input으로부터 동요되는 것을 방지할 수 있고, output gate unit은 현재 unit j의 정보가 마찬가지로 다른 unit의 정보에 영향을 끼치는 것을 조절할 수 있는 구조이다.
*carrousel: 사전적 의미로 수하물 운반 벨트를 의미하며, 정보가 컨베이어 벨트처럼 연속적으로 한 방향으로 흐름을 의미

위 그림(Fig.1)은 각 memory cell의 구조를 나타낸 것이다. 여기서 하나의 직사각형 내부를 memory cell이라 하며 c_j로 표시되어 있다. 각 cell은 input gate(in_j)와 output gate(out_j) 모두에게 input 신호를 받는다.
In_j의 시간 t에 따른 활성화 여부를 y^in_j (t), out_j의 시간 t에 따른 활성화 여부를 y^out_j (t)라고 할 때, 각각을 다음과 같이 표현할 수 있다.

여기서 u는 input gate, gate unit, memory cell, convention hidden units에 해당하는 index이다. Input gate 또는 output gate는 다른 memory cell에서 넘어온 input 신호를 현 memory cell에서 어디에 저장할지 결정할 수 있다.
이 memory cell을 거친 출력값 y^{c_j} (t)는 아래와 같이 계산되며, internal state의 값도 아래와 같이 계산된다.

Why gate units?
그렇다면 왜 gate unit을 쓰는가? In_j는 정보를 c_j안에 보관하도록 하거나 정보의 유입을 차단할 수 있다. 반대로 out_j는 현재 c_j안에서 액세스 하거나 다른 unit들이 c_j로 영향 받는 여부를 결정할 수 있다. 이를 이용해 가중치(weights)가 서로 충돌하는 것을 방지할 수 있다.
Error signal이 한 번 memory cell의 CEC에 들어오면 그 값은 변할 수 없다. 이 때, 다른 때 들어오는 신호와 겹치면 문제가 발생할 수 있으므로, output gate는 scaling을 통해 어떤 error signal을 CEC에 보관할 지 학습해야한다. 마찬가지로 input gate는 언제 error signal을 넘길지 scaling을 통해 학습한다. 이렇게 input, output gate를 모두 활용함으로써 long time lag memory가 short time lag memory로인해 간섭 받는 것을 방지할 수 있다.
Network Topology
네트워크 구조(Network Topology)는 다음과 같다, 각 네트워크당 하나의 input layer, hidden layer, output layer가 있다. 이 중에서 (fully) self-connected hidden layer가 상기한 memory cells를 포함하고 있다 (추가적으로 conventional hidden unit을 포함하고 있는 경우도 있다). 또한, 이 memory cell들이 같은 input gate와 같은 output gate를 공유하면 그 크기를 S라고 한다. 크기가 1인 경우, 단순(simple) memory cell이라고 한다.
Learning
이 네트워크의 학습 방식은 RTRL(e.g., Robinson and Fallside 1987)의 변형된 형태를 따른다. 여기서 소멸하지 않는(non-decaying) error backpropagation 을 보장하기 위해 한 번 memory cell의 net input을 통과한 error signal은 절대로 propagate 되지 않는다. 단, memory cell 내부에서의 propagation은 가능하다.

Fig.2는 input의 한 unit과 연결된 hidden layer, output unit을 그림으로 나타낸 예시이다. 연결된 수 많은 node중에 back propagation을 위한 node가 연결되어 있지 않다.
Time Complexity
이 네트워크의 시간 복잡도는 O(W)로, 여기서 W는 weight의 수를 의미한다. 왜냐하면, weight에따른 internal state의 편미분 값만 업데이트 되고, activation value를 새로 업데이트할 필요가 없기 때문이다.
초기의 학습 단계에서 정보의 저장 없이도 error reduction이 발생할 수 있는데, 이 때 network 내에서 정보가 memory cell에 저장되지 않는(Abuse problem)이 발생할 수 있다. 그리고 이들이 다시 학습 가능하도록 release하는데 오랜 시간이 걸릴 수 있다는 단점이 있다. 이 문제나 유사한 문제가 발생했을 때 Sequential network construction*이나 Output gate bias**를 통해 개선이 가능하다
*memory cell과 대응되는 gate unit들이 error의 감소가 멈추었을 때만 추가됨
**각 output gate가 음의 초기 편차를 가져 초기 memory cell activation을 0으로 향하게 한다
#Internal state drive and remedies
만일 memory cell의 c_j의 input이 대부분 양이거나 대부분 음인 경우, gradient가 0으로 빠르게 수렴하는 문제가 발생한다. 이를 해결하기 위해 적절한 활성화 함수 h를 선택하는 것이 중요하다. 또는 in_j의 초기 편향을 0에 가깝게 하는 것도 도움이 될 수 있다.
'2023 Summer Session > DL' 카테고리의 다른 글
| [6주차/DL2팀/논문리뷰] Attention is all you need (1) | 2023.08.19 |
|---|---|
| [5주차/DL1팀/논문 리뷰] Gated Recurrent Neural Network (0) | 2023.08.09 |
| [4주차/DL2팀/논문 리뷰] (0) | 2023.08.08 |
| [4주차 / DL 1팀 / 논문 리뷰 ] Deep Residual Learning for Image Recognition (0) | 2023.08.03 |
| [3주차/DL1팀/논문 리뷰] Batch Normalization (0) | 2023.07.27 |





댓글 영역