[4주차 / 박민규 / 논문리뷰] Generative Adversial Nets

GAN

이미지 데이터는 다차원 feature space의 한점으로 표현할 수 있으며, 이미지의 문포를 근사하는 모델을 학습할 수 있다.

사람의 얼굴에는 통계적인 평균치가 존재하는데 모델은 이를 수치적으로 표현할 수 있다.

GAN은 image에 대해서 다변수확률로써 확률분포를 학습한다. feature map 상에서 확률분포는 다음과 같다.

Generative Model은 실존하지 않지만 있을 법한 이미지를 생성할 수 있는 모델을 의미한다.

확률분포를 잘 학습할 수 있다면, GAN 모델은 통계적인 평균치를 내제하여 확률 값이 높은 부분을 sampling하면 있음직한 이미지를 얻을 수 있다.

생성 모델의 목표는 image data의 distribution을 근사하는 모델 G를 만드는 것이며, 모델 G는 원본 데이터(image)의 분포를 학습한다.

모델이 잘 학습되었다면 원본 데이터의 분포를 잘 근사할 수 있으며, 통계적으로 평균적인 feature특징을 가지는 데이터를 쉽게 생성할 수 있다.

Object Function

GAN은 생성자generator와 판별자discriminator 두 개의 네트워크를 활용한 생성 모델이다. Objective function을 통해 생성자는 원본 데이터의 분포를 학습할 수 있다.

GAN 모델에서 있음직한 이미지를 생성하기 위해 생성자G를 이용하며 판별자D는 생성자가 잘 학습될 수 있도록 도와주는 역할을 한다.

Gnerator($G(z)$) noise 분포에에서 한개의 data z를 sampling한 후, 새로운 image instance를 만든다.

Discriminator($D(x)$) 원본 data의 분포에서 한개의 data x를 sampling한 후, 해당 이미지가 얼마나 진짜 같은가에 대한 확률을 출력한다. real로 판별하면 1, fake로 판별하면 0의 출력값이 나온다.

목적함수의 좌항 원본 data의 분포에서 여러개의 x를 sampling하고 판별자를 거쳐 나온 진짜일 확률의 로그평균을 의미한다.

목적함수의 우항 noise data의 분포에서 여러개의 z를 sampling하고 생성자로 새로운 image를 만들고, 판별자를 거쳐나온 가짜일 확률의 로그평균을 의미한다.

Objective function은 원본 데이터(image)에 대해서 판별자D가 1로 분류할 수 있도록, fake image에 대해서는 판별자D가 0으로 분류할 수 있도록 학습하며,

동시에 생성자G가 만든 fake image를 판별자D가 진짜라고 판별하여 1로 분류하도록 학습한다.

학습과정

동일한 식에 대하여 G와 D의 목적이 다르기 때문에 게임이론 기반의 minmax optimization 문제로 볼 수 있다.

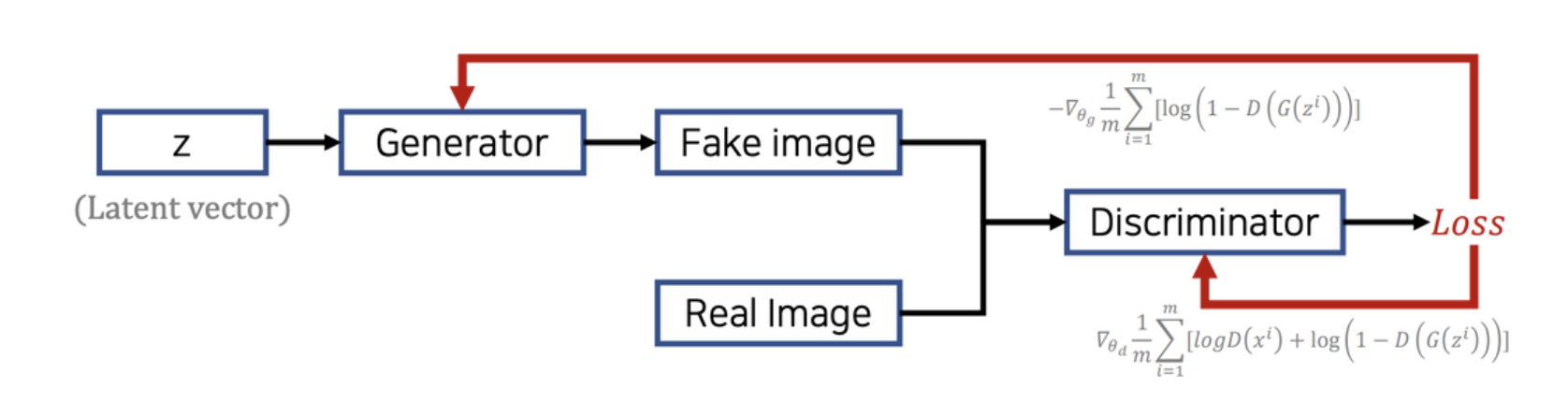
noise vector에서 sampling한 z가 들어오면, Generator가 fake image를 만든다.

Discirminator의 input으로 fake image와 fake image와 mapping되는 real image가 들어가서 loss를 계산한다.

그리고 loss가 줄어드는 방향으로 G를 update한다. 이때 learning rate($\nabla_{\theta_g}$) * $\frac{\partial loss\ function}{\partial G}$ 값만큼 음의 방향으로 update 해준다. ⇒ gradient descent

이와 동시에 real image는 1으로 분류하고, fake image는 0으로 분류할 수 있게끔 D를 update한다. 이때 learning rate ($\nabla_{\theta_d}$) * $\frac{\partial loss\ function}{\partial D}$ 값만큼 양의 방향으로 update gownsek. ⇒ gradient ascent

실제 모델을 학습할 때 D먼저 학습 후 G를 학습하거나, G먼저 학습 후 D를 학습하거나 이렇게 매번 mini-batch 두 network의 학습 순서를 번갈아가며 반복한다.

이렇게 D,G 모두 optimal point에 도달할 수 있도록 학습을 유도한다.

증명

GAN은 생성자의 분포가 원본 학습데이터의 분포를 잘 따를 수 있도록 만드는 것이 목표이다.

$P_g$(생성자의 분포)가 $P_{data}$(원본의 분포)에 수렴한다면, D는 G가 생성한 fake image가 진짜인지 가짜인지 구별불가능하다. ⇒ $D(G(z))=\frac{1}{2}$ 에 수렴하게 된다.

• (a)에서는 생성자의 분포가 원본 data의 분포를 아직은 잘 학습하지 못하였기 때문에, 파란색 점선에 해당하는 discriminator가 fake image를 잘 구분한다.
• 학습이 진행될수록 생성자가 학습한 분포가 원본 데이터의 분포를 따라간다.
• (d)에서는 생성자가 학습한 분포와 원본 데이터의 분포가 수렴하고, 판별 모델의 분포가 1/2로 수렴하게 된다.

학습이 끝난 후(d) 검은색 점에 해당하지 않은 영역의 데이터를 시각화하면, GAN 모델이 생성한 있음직한 image를 볼 수 있다.

이를 위해 학습이 진행될수록 $P_g$가 $P_{data}$에 수렴할 수 있는 이유를 증명해야 한다.

D 수렴가능성

G를 고정했을 때, D는 $\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$ 분포를 가질 때 목적함수(V)가 최대화된다.

• 주황 화살표

z domain에서 sampling된 noise 값들을 생성자G에 넣어 나온 출력값은 data “x”의 확률분포에 근사할 수 있다. 즉, domain z에서 x로 mapping할 수 있다.

마지막 식을 미분하여 0인 지점을 찾으면 [0,1]에서 V(G,D)가 극대값을 갖는 지점은 $\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$임을 알 수 있다.

Global optimum point

우리가 궁극적으로 알고지하는것은 생성자G의 global optimal point이다.

C(G)는 global optimal을 가지는 D함수($D^*)$로 이루어진 G에 대한 함수이다.

JSD는 일종의 distance metric이기 때문에 최소값은 0이며, global optimal point인 -log(4)가 되기 위해선 p_{data}=p_g를 만족해야 한다.

알고리즘

• 앞단에 정의한 epoch를 통해 몇번 반복할지를 정한다.
• epoch 당 k번 D를 학습한다. (mini-batch의 개수=k)
• mini-batch당 m개의 noise를 sampling하고, m개의 원본 데이터를 sampling한다. 그리고 주황색만큼 gradient ascending을 진행하여 D를 학습한다.
• D학습이 끝나면 G를 학습한다. (1번)
• m개의 noise를 sampling하고 sampling한 noise로 m개의 fake image를 만든다. 그리고 초록색만큼 gradient descending을 진행하여 G를 학습한다.